[book] Python Data Science Handbook

[book] Python Data Science Handbook#

A study note of [VanderPlas, 2016]

1. Numpy#

Data types in Python :snake:#

输入图片描述

Fixed-type NumPy-style arrays lack this flexibility, but are much more efficient for storing and manipulating data.
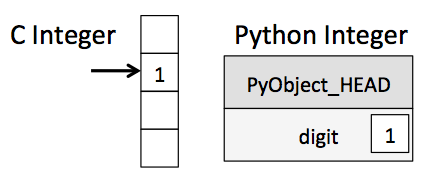
The standard Python implementation is written in C. This means that every Python object is simply a cleverly-disguised C structure, which contains not only its value, but other information as well.
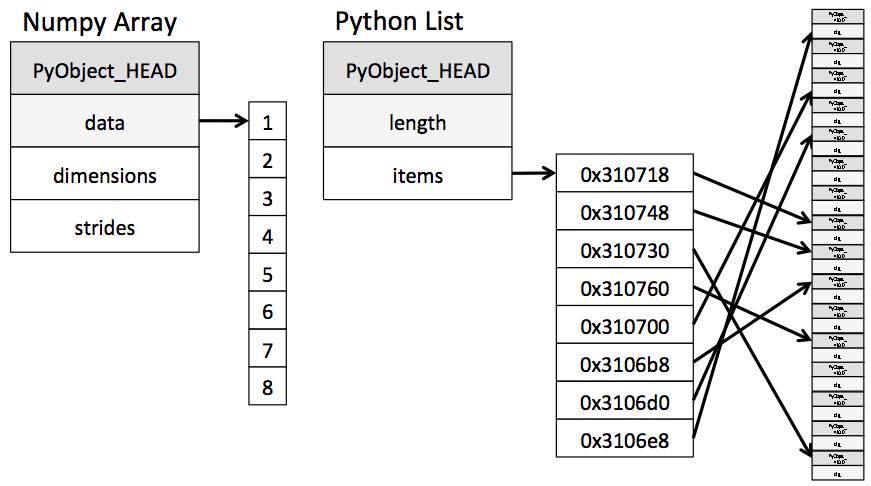
A Python integer is a pointer to a position in memory containing all the Python object information, including the bytes that contain the integer value. This extra information in the Python integer structure is what allows Python to be coded so freely and dynamically. All this additional information in Python types comes at a cost, however, which becomes especially apparent in structures that combine many of these objects.
Much more useful, however, is the ndarray object of the NumPy package. While Python’s array object provides efficient storage of array-based data, NumPy adds to this efficient operations on that data.

Basics of NumPy arrays#

TOC

np arrary attributes: dimension, shape, size, dtype, itemsize, etc.
Array indexing: Accessing Single Elements
Array Slicing: Accessing Subarrays
- one-dimensional array
- multi-dimensional
Reshaping of Arrays
Array Concatenation and Splitting

The NumPy slicing syntax follows that of the standard Python list; to access a slice of an array x, use this:

x[start:stop:step]

If any of these are unspecified, they default to the values start=0, stop=size of dimension, step=1.
Other attributes include itemsize, which lists the size (in bytes) of each array element, and nbytes, which lists the total size (in bytes) of the array
In a multi-dimensional array, items can be accessed using a comma-separated tuple of indices:

x2
>>> array([[3, 5, 2, 4],
       [7, 6, 8, 8],
       [1, 6, 7, 7]])
       
x2[0, 0]
>>> 3

In slicing, a potentially confusing case is when the step value is negative. In this case, the defaults for start and stop are swapped. This becomes a convenient way to reverse an array. (便捷地反转一个array的方法)
Keep in mind that, unlike Python lists, NumPy arrays have a fixed type. This means, for example, that if you attempt to insert a floating-point value to an integer array, the value will be silently truncated.
One important–and extremely useful–thing to know about array slices is that they return views rather than copies of the array data. This is one area in which NumPy array slicing differs from Python list slicing: in lists, slices will be copies.
If we modify the subarray, we’ll see that the original array is changed! This default behavior is actually quite useful: it means that when we work with large datasets, we can access and process pieces of these datasets without the need to copy the underlying data buffer.
In the case of row access, the empty slice can be omitted for a more compact syntax:

print(x2[0])  # equivalent to x2[0, :]

Another common reshaping pattern is the conversion of a one-dimensional array into a two-dimensional row or column matrix. This can be done with the reshape method, or more easily done by making use of the newaxis keyword within a slice operation:

x = np.array([1, 2, 3])

# row vector via reshape
x.reshape((1, 3))

# row vector via newaxis
x[np.newaxis, :]

Computation on NumPy Arrays: Universal Functions#

TOC

The Slowness of Loops
Introducing UFuncs
Exploring NumPy’s UFuncs
- Array arithmetic
- Absolute value
- Trigonometric functions
- Exponents and logarithms
- Specialized ufuncs
Advanced Ufunc Features
- Specifying output
- Aggregates
- Outer products
Ufuncs: Learning More

Vectorized operations in NumPy are implemented via ufuncs, whose main purpose is to quickly execute repeated operations on values in NumPy arrays. Ufuncs are extremely flexible – before we saw an operation between a scalar and an array, but we can also operate between two arrays
Ufuncs exist in two flavors: unary ufuncs, which operate on a single input, and binary ufuncs, which operate on two inputs.
Each of these arithmetic operations are simply convenient wrappers around specific functions built into NumPy
The following table lists the arithmetic operators implemented in NumPy:

Operator	Equivalent ufunc	Description
`+`	`np.add`	Addition (e.g., `1 + 1 = 2`)
`-`	`np.subtract`	Subtraction (e.g., `3 - 2 = 1`)
`-`	`np.negative`	Unary negation (e.g., `-2`)
`*`	`np.multiply`	Multiplication (e.g., `2 * 3 = 6`)
`/`	`np.divide`	Division (e.g., `3 / 2 = 1.5`)
`//`	`np.floor_divide`	Floor division (e.g., `3 // 2 = 1`)
`**`	`np.power`	Exponentiation (e.g., `2 ** 3 = 8`)
`%`	`np.mod`	Modulus/remainder (e.g., `9 % 4 = 1`)

There are also some specialized versions that are useful for maintaining precision with very small input:

x = [0, 0.001, 0.01, 0.1]
print("exp(x) - 1 =", np.expm1(x))
print("log(1 + x) =", np.log1p(x))

>>> exp(x) - 1 = [ 0.          0.0010005   0.01005017  0.10517092]
>>> log(1 + x) = [ 0.          0.0009995   0.00995033  0.09531018]

When x is very small, these functions give more precise values than if the raw np.log or np.exp were to be used.

Specifying the output:

y = np.zeros(10)
np.power(2, x, out=y[::2])
print(y) 

>>> [  1.   0.   2.   0.   4.   0.   8.   0.  16.   0.]

If we had instead written y[::2] = 2 ** x, this would have resulted in the creation of a temporary array to hold the results of 2 ** x, followed by a second operation copying those values into the y array. This doesn’t make much of a difference for such a small computation, but for very large arrays the memory savings from careful use of the out argument can be significant.

Another excellent source for more specialized and obscure ufuncs is the submodule scipy.special. If you want to compute some obscure mathematical function on your data, chances are it is implemented in scipy.special.
The ufunc.at and ufunc.reduceat methods, which we’ll explore in Fancy Indexing, are very helpful as well.
More information on universal functions (including the full list of available functions) can be found on the NumPy and SciPy documentation websites.

Aggregations: Min, Max, and Everything In Between#

TOC

Summing the Values in an Array
Minimum and Maximum
- Multi dimensional aggregates
- Other aggregation functions

For min, max, sum, and several other NumPy aggregates, a shorter syntax is to use methods of the array object itself:

print(big_array.min(), big_array.max(), big_array.sum())

The axis keyword specifies the dimension of the array that will be collapsed, rather than the dimension that will be returned. So specifying axis=0 means that the first axis will be collapsed: for two-dimensional arrays, this means that values within each column will be aggregated.
Most aggregates have a NaN-safe counterpart that computes the result while ignoring missing values, which are marked by the special IEEE floating-point NaN value (for a fuller discussion of missing data, see Handling Missing Data).The following table provides a list of useful aggregation functions available in NumPy:

Function Name	NaN-safe Version	Description
np.sum	np.nansum	Compute sum of elements
np.prod	np.nanprod	Compute product of elements
np.mean	np.nanmean	Compute mean of elements
np.std	np.nanstd	Compute standard deviation
np.var	np.nanvar	Compute variance
np.min	np.nanmin	Find minimum value
np.max	np.nanmax	Find maximum value
np.argmin	np.nanargmin	Find index of minimum value
np.argmax	np.nanargmax	Find index of maximum value
np.median	np.nanmedian	Compute median of elements
np.percentile	np.nanpercentile	Compute rank-based statistics of elements
np.any	N/A	Evaluate whether any elements are true
np.all	N/A	Evaluate whether all elements are true

Computation on Arrays: Broadcasting#

TOC

Introducing Broadcasting
Rules of Broadcasting
- Broadcasting examples 1/2/3
Broadcasting in Practice
- Centering an array
- Plotting a two-dimensional function

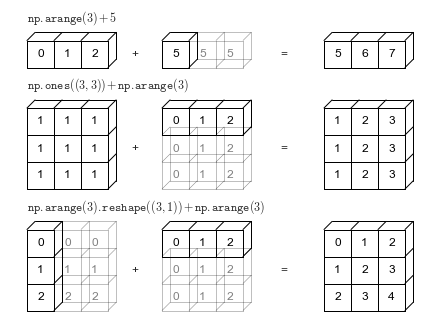
Broadcasting is simply a set of rules for applying binary ufuncs (e.g., addition, subtraction, multiplication, etc.) on arrays of different sizes.
For arrays of the same size, binary operations are performed on an element-by-element basis
The advantage of NumPy’s broadcasting is that this duplication of values does not actually take place, but it is a useful mental model as we think about broadcasting.
Broadcasting in NumPy follows a strict set of rules to determine the interaction between the two arrays:
- Rule 1: If the two arrays differ in their number of dimensions, the shape of the one with fewer dimensions is padded with ones on its leading (left) side.
- Rule 2: If the shape of the two arrays does not match in any dimension, the array with shape equal to 1 in that dimension is stretched to match the other shape.
- Rule 3: If in any dimension the sizes disagree and neither is equal to 1, an error is raised.

Comparisons, Masks, and Boolean Logic#

TOC

Example
Comparison Operators as ufuncs
Working with Boolean Arrays
- Counting entries
- Boolean operators
Boolean Arrays as Masks
Aside: Using the Keywords and/or Versus the Operators &/|

A quick warning: as mentioned in Aggregations: Min, Max, and Everything In Between, Python has built-in sum(), any(), and all() functions. These have a different syntax than the NumPy versions, and in particular will fail or produce unintended results when used on multidimensional arrays. Be sure that you are using np.sum(), np.any(), and np.all() for these examples!
When you use and or or, it’s equivalent to asking Python to treat the object as a single Boolean entity. So remember this: and and or perform a single Boolean evaluation on an entire object, while & and | perform multiple Boolean evaluations on the content (the individual bits or bytes) of an object. For Boolean NumPy arrays, the latter is nearly always the desired operation.

Fancy Indexing#

TOC

Exploring Fancy Indexing
Combined Indexing
Example: Selecting Random Points
Modifying Values with Fancy Indexing
Example: Binning Data

Fancy indexing is like the simple indexing we’ve already seen, but we pass arrays of indices in place of single scalars. This allows us to very quickly access and modify complicated subsets of an array’s values.
When using fancy indexing, the shape of the result reflects the shape of the index arrays rather than the shape of the array being indexed:

ind = np.array([[3, 7],
                [4, 5]])
x[ind]

>>> array([[71, 86],
       [60, 20]])

It is always important to remember with fancy indexing that the return value reflects the broadcasted shape of the indices, rather than the shape of the array being indexed.
One common use of fancy indexing is the selection of subsets of rows from a matrix.

indices = np.random.choice(X.shape[0], 20, replace=False)
selection = X[indices]  # fancy indexing here
selection.shape
>>> (20, 2)

print(x)
>>> [ 6.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
i = [2, 3, 3, 4, 4, 4]
x[i] += 1
x
>>> array([ 6.,  0.,  1.,  1.,  1.,  0.,  0.,  0.,  0.,  0.])

x[i] += 1 is meant as a shorthand of x[i] = x[i] + 1. x[i] + 1 is evaluated, and then the result is assigned to the indices in x. With this in mind, it is not the augmentation that happens multiple times, but the assignment, which leads to the rather nonintuitive results.
What if you want the other behavior where the operation is repeated? For this, you can use the at() method of ufuncs (available since NumPy 1.8), and do the following:

i = [2, 3, 3, 4, 4, 4]
x = np.zeros(10)
np.add.at(x, i, 1)
print(x)
>>> [ 0.  0.  1.  2.  3.  0.  0.  0.  0.  0.]

The pairing of indices in fancy indexing follows all the broadcasting rules that were mentioned in Computation on Arrays: Broadcasting.

Sorting Arrays#

TOC

Fast Sorting in NumPy: np.sort and np.argsort
- Sorting along rows or columns
Partial Sorts: Partitioning
Example: k-Nearest Neighbors
Aside: Big-O Notation

As any first-year computer science major will tell you, the selection sort is useful for its simplicity, but is much too slow to be useful for larger arrays. For a list of $N$ values, it requires $N$ loops, each of which does on order $\sim N$ comparisons to find the swap value. In terms of the “big-O” notation often used to characterize these algorithms (see Big-O Notation), selection sort averages $\mathcal{O}[N^2]$: if you double the number of items in the list, the execution time will go up by about a factor of four.
By default np.sort uses an $\mathcal{O}[N \mathcal{log}N]$ , quicksort algorithm, though mergesort and heapsort are also available. For most applications, the default quicksort is more than sufficient.
To return a sorted version of the array without modifying the input, you can use np.sort

x = np.array([2, 1, 4, 3, 5])
np.sort(x)
>>> array([1, 2, 3, 4, 5])

A related function is argsort, which instead returns the indices of the sorted elements:

x = np.array([2, 1, 4, 3, 5])
i = np.argsort(x)
print(i)
>>> [1 0 3 2 4]

If you prefer to sort the array in-place, you can instead use the sort method of arrays:

x.sort()
print(x)
>>> [1 2 3 4 5]

Sometimes we’re not interested in sorting the entire array, but simply want to find the k smallest values in the array. NumPy provides this in the np.partition function. np.partition takes an array and a number K; the result is a new array with the smallest K values to the left of the partition, and the remaining values to the right, in arbitrary order.

x = np.array([7, 2, 3, 1, 6, 5, 4])
np.partition(x, 3)
>>> array([2, 1, 3, 4, 6, 5, 7])

Big-O notation, in this loose sense, tells you how much time your algorithm will take as you increase the amount of data. If you have an $\mathcal{O}[N]$ (read “order $N$”) algorithm that takes 1 second to operate on a list of length N=1,000, then you should expect it to take roughly 5 seconds for a list of length N=5,000. If you have an $\mathcal{O}[N^2]$ (read “order N squared”) algorithm that takes 1 second for N=1000, then you should expect it to take about 25 seconds for N=5000.
Notice that the big-O notation by itself tells you nothing about the actual wall-clock time of a computation, but only about its scaling as you change N. Generally, for example, an $\mathcal{O}[N]$ algorithm is considered to have better scaling than an $\mathcal{O}[N^2]$ algorithm, and for good reason. But for small datasets in particular, the algorithm with better scaling might not be faster.

Structured Data: NumPy’s Structured Arrays#

less important - use more pandas instead of numpy structed array

TOC

Creating Structured Arrays
More Advanced Compound Types
RecordArrays: Structured Arrays with a Twist
On to Pandas

The handy thing with structured arrays is that you can now refer to values either by index or by name
If the names of the types do not matter to you, you can specify the types alone in a comma-separated string

np.dtype('S10,i4,f8')
>>> dtype([('f0', 'S10'), ('f1', '<i4'), ('f2', '<f8')])

The shortened string format codes may seem confusing, but they are built on simple principles. The first (optional) character is < or >, which means “little endian” or “big endian,” respectively, and specifies the ordering convention for significant bits. The next character specifies the type of data: characters, bytes, ints, floating points, and so on (see the table below). The last character or characters represents the size of the object in bytes.

Character	Description	Example
‘b’	Byte	np.dtype(‘b’)
‘i’	Signed integer	np.dtype(‘i4’) == np.int32
‘u’	Unsigned integer	np.dtype(‘u1’) == np.uint8
‘f’	Floating point	np.dtype(‘f8’) == np.int64
‘c’	Complex floating point	np.dtype(‘c16’) == np.complex128
‘S’, ‘a’	String	np.dtype(‘S5’)
‘U’	Unicode string	np.dtype(‘U’) == np.str_
‘V’	Raw data (void)	np.dtype(‘V’) == np.void

2. Pandas :panda_face:#

Introducing Pandas Objects#

TOC

The Pandas Series Object
- Series as generalized NumPy array
- Series as specialized dictionary
- Constructing Series objects
The Pandas DataFrame Object
- DataFrame as a generalized NumPy array
- DataFrame as specialized dictionary
- Constructing DataFrame objects
  - From a single Series object
  - From a list of dicts
  - From a dictionary of Series objects
  - From a two-dimensional NumPy array
  - From a NumPy structured array
The Pandas Index Object
- Index as immutable array
- Index as ordered set

A Pandas Series is a one-dimensional array of indexed data.
At the very basic level, Pandas objects can be thought of as enhanced versions of NumPy structured arrays in which the rows and columns are identified with labels rather than simple integer indices. (series as generalized Numpy array)
You can think of a Pandas Series a bit like a specialization of a Python dictionary. A dictionary is a structure that maps arbitrary keys to a set of arbitrary values, and a Series is a structure which maps typed keys to a set of typed values. This typing is important: just as the type-specific compiled code behind a NumPy array makes it more efficient than a Python list for certain operations, the type information of a Pandas Series makes it much more efficient than Python dictionaries for certain operations. (series as specilized dictionary)
Unlike a dictionary, though, the Series also supports array-style operations such as slicing (using its index)
It may look like the Series object is basically interchangeable with a one-dimensional NumPy array. The essential difference is the presence of the index: while the Numpy Array has an implicitly defined integer index used to access the values, the Pandas Series has an explicitly defined index associated with the values.
As we see in the output, the Series wraps both a sequence of values and a sequence of indices, which we can access with the values and index attributes. The values are simply a familiar NumPy array
The pandas Series index is an array-like object of type pd.Index

data.index
>>> RangeIndex(start=0, stop=4, step=1)

Data Indexing and Selection#

TOC

Data Selection in Series
- Series as dictionary
- Series as one-dimensional array
- Indexers: loc, iloc, and ix
Data Selection in DataFrame
- DataFrame as a dictionary
- DataFrame as two-dimensional array
- Additional indexing conventions

There are a couple extra indexing conventions that might seem at odds with the preceding discussion, but nevertheless can be very useful in practice. First, while indexing refers to columns, slicing refers to rows
Pandas provides some special indexer attributes, these are not functional methods, but attributes that expose a particular slicing interface to the data in the Series.
the loc attribute allows indexing and slicing that always references the explicit index, this means explicit index and column names in DataFrames.
The iloc attribute allows indexing and slicing that always references the implicit Python-style index
A third indexing attribute, ix, is a hybrid of the two, and for Series objects is equivalent to standard []-based indexing. The purpose of the ix indexer will become more apparent in the context of DataFrame objects, where both implicit index or expilcit index and column name can be used.

data = pd.Series(['a', 'b', 'c'], index=[1, 3, 5])
data

>>> 
1    a
3    b
5    c
dtype: object

data.loc[1]
>>> 'a'

data.iloc[1]
>>> 'b'

One guiding principle of Python code is that “explicit is better than implicit.” The explicit nature of loc and iloc make them very useful in maintaining clean and readable code
a DataFrame acts in many ways like a two-dimensional or structured array, and in other ways like a dictionary of Series structures sharing the same index. These analogies can be helpful to keep in mind as we explore data selection within this structure.
we can use attribute-style access with column names that are strings

data.area
>>> 
California    423967
Florida       170312
Illinois      149995
New York      141297
Texas         695662
Name: area, dtype: int64

Avoid the temptation to try column assignment via attribute (i.e., use data[‘pop’] = z rather than data.pop = z)

Operating on Data in Pandas#

TOC

Ufuncs: Index Preservation
UFuncs: Index Alignment
- Index alignment in Series
- Index alignment in DataFrame
Ufuncs: Operations Between DataFrame and Series

Pandas includes a couple useful twists, however: for unary operations like negation and trigonometric functions, these ufuncs will preserve index and column labels in the output, and for binary operations such as addition and multiplication, Pandas will automatically align indices when passing the objects to the ufunc.
For binary operations on two Series or DataFrame objects, Pandas will align indices in the process of performing the operation. This is very convenient when working with incomplete data
Any item for which one or the other does not have an entry is marked with NaN, or “Not a Number,” which is how Pandas marks missing data (see further discussion of missing data in Handling Missing Data). This index matching is implemented this way for any of Python’s built-in arithmetic expressions; any missing values are filled in with NaN by default
If using NaN values is not the desired behavior, the fill value can be modified using appropriate object methods in place of the operators.

A.add(B, fill_value=0)
>>>
0    2.0
1    5.0
2    9.0
3    5.0
dtype: float64

This preservation and alignment of indices and columns means that operations on data in Pandas will always maintain the data context, which prevents the types of silly errors that might come up when working with heterogeneous and/or misaligned data in raw NumPy arrays.

Handling Missing Data#

TOC

Trade-Offs in Missing Data Conventions
Missing Data in Pandas
- None: Pythonic missing data
- NaN: Missing numerical data
- NaN and None in Pandas
Operating on Null Values
- Detecting null values
- Dropping null values
- Filling null values

- There are a number of schemes that have been developed to indicate the presence of missing data in a table or DataFrame. Generally, they revolve around one of two strategies: using a mask that globally indicates missing values, or choosing a sentinel value that indicates a missing entry. None of these approaches is without trade-offs: use of a separate mask array requires allocation of an additional Boolean array, which adds overhead in both storage and computation. A sentinel value reduces the range of valid values that can be represented, and may require extra (often non-optimized) logic in CPU and GPU arithmetic. Common special values like NaN are not available for all data types.

With these constraints in mind, Pandas chose to use sentinels for missing data, and further chose to use two already-existing Python null values: the special floating-point NaN value, and the Python None object. This choice has some side effects, as we will see, but in practice ends up being a good compromise in most cases of interest.
The way in which Pandas handles missing values is constrained by its reliance on the NumPy package, which does not have a built-in notion of NA values for non-floating-point data types.
Because it is a Python object, None cannot be used in any arbitrary NumPy/Pandas array, but only in arrays with data type ‘object’ (i.e., arrays of Python objects)

vals1 = np.array([1, None, 3, 4])
vals1
>>> array([1, None, 3, 4], dtype=object)

This dtype=object means that the best common type representation NumPy could infer for the contents of the array is that they are Python objects. While this kind of object array is useful for some purposes, any operations on the data will be done at the Python level, with much more overhead than the typically fast operations seen for arrays with native types.

The use of Python objects in an array also means that if you perform aggregations like sum() or min() across an array with a None value, you will generally get an error
The following table lists the upcasting conventions in Pandas when NA values are introduced:

Typeclass	Conversion When Storing NAs	NA Sentinel Value
`floating`	No change	`np.nan`
`object`	No change	`None` or `np.nan`
`integer`	Cast to `float64`	`np.nan`
`boolean`	Cast to object	`None` or `np.nan`

Keep in mind that in Pandas, string data is always stored with an object dtype.
The other missing data representation, NaN (acronym for Not a Number), is different; it is a special floating-point value recognized by all systems that use the standard IEEE floating-point representation

vals2 = np.array([1, np.nan, 3, 4]) 
vals2.dtype
>>> dtype('float64')

Notice that NumPy chose a native floating-point type for this array: this means that unlike the object array from before, this array supports fast operations pushed into compiled code. You should be aware that NaN is a bit like a data virus–it infects any other object it touches.
Keep in mind that NaN is specifically a floating-point value; there is no equivalent NaN value for integers, strings, or other types.
Pandas treats None and NaN as essentially interchangeable for indicating missing or null values. To facilitate this convention, there are several useful methods for detecting, removing, and replacing null values in Pandas data structures.
- isnull(): Generate a boolean mask indicating missing values
- notnull(): Opposite of isnull()
- dropna(): Return a filtered version of the data
- fillna(): Return a copy of the data with missing values filled or imputed
- In addition to the masking used before, there are the convenience methods, dropna() (which removes NA values) and fillna() (which fills in NA values)
By default, dropna() will drop all rows in which any null value is present; you might rather be interested in dropping rows or columns with all NA values, or a majority of NA values. This can be specified through the how or thresh parameters, which allow fine control of the number of nulls to allow through.

df.dropna(axis='columns', how='all')
df.dropna(axis='rows', thresh=3)

Hierarchical Indexing#

TOC

A Multiply Indexed Series
- The bad way
- The Better Way: Pandas MultiIndex
- MultiIndex as extra dimension
Methods of MultiIndex Creation
- Explicit MultiIndex constructors
- MultiIndex level names
- MultiIndex for columns
Indexing and Slicing a MultiIndex
- Multiply indexed Series
- Multiply indexed DataFrames
Rearranging Multi-Indices
- Sorted and unsorted indices
- Stacking and unstacking indices
- Index setting and resetting
Data Aggregations on Multi-Indices
Aside: Panel Data

While Pandas does provide Panel and Panel4D objects that natively handle three-dimensional and four-dimensional data (see Aside: Panel Data), a far more common pattern in practice is to make use of hierarchical indexing (also known as multi-indexing) to incorporate multiple index levels within a single index. In this way, higher-dimensional data can be compactly represented within the familiar one-dimensional Series and two-dimensional DataFrame objects.
The most straightforward way to construct a multiply indexed Series or DataFrame is to simply pass a list of two or more index arrays to the constructor.
Pandas is built with this equivalence in mind. The unstack() method will quickly convert a multiply indexed Series into a conventionally indexed DataFrame and naturally, the stack() method provides the opposite operation

pop_df = pop.unstack()
pop = pop_df.stack()

Seeing this, you might wonder why would we would bother with hierarchical indexing at all. The reason is simple: just as we were able to use multi-indexing to represent two-dimensional data within a one-dimensional Series, we can also use it to represent data of three or more dimensions in a Series or DataFrame. Each extra level in a multi-index represents an extra dimension of data; taking advantage of this property gives us much more flexibility in the types of data we can represent.

df = pd.DataFrame(np.random.rand(4, 2),
                  index=[['a', 'a', 'b', 'b'], [1, 2, 1, 2]],
                  columns=['data1', 'data2'])
df

	data1	data2
a	1	0.554233	0.356072
	2	0.925244	0.219474
b	1	0.441759	0.610054
	2	0.171495	0.886688

The work of creating the MultiIndex is done in the background. Similarly, if you pass a dictionary with appropriate tuples as keys, Pandas will automatically recognize this and use a MultiIndex by default:

data = {('California', 2000): 33871648,
        ('California', 2010): 37253956,
        ('Texas', 2000): 20851820,
        ('Texas', 2010): 25145561,
        ('New York', 2000): 18976457,
        ('New York', 2010): 19378102}
pd.Series(data)

>>>
California  2000    33871648
            2010    37253956
New York    2000    18976457
            2010    19378102
Texas       2000    20851820
            2010    25145561
dtype: int64

For more flexibility in how the index is constructed, you can instead use the class method constructors available in the pd.MultiIndex:

pd.MultiIndex.from_arrays([['a', 'a', 'b', 'b'], [1, 2, 1, 2]])
pd.MultiIndex.from_tuples([('a', 1), ('a', 2), ('b', 1), ('b', 2)])

For various reasons, partial slices and other similar operations require the levels in the MultiIndex to be in sorted (i.e., lexographical) order. Pandas provides a number of convenience routines to perform this type of sorting; examples are the sort_index() and sortlevel() methods of the DataFrame:

data = data.sort_index()

Remember that columns are primary in a DataFrame, and the syntax used for multiply indexed Series applies to the columns.
Another way to rearrange hierarchical data is to turn the index labels into columns; this can be accomplished with the reset_index method.

pop_flat = pop.reset_index(name='population')

We’ve previously seen that Pandas has built-in data aggregation methods, such as mean(), sum(), and max(). For hierarchically indexed data, these can be passed a level parameter that controls which subset of the data the aggregate is computed on.

data_mean = health_data.mean(level='year') #average over the year

By further making use of the axis keyword, we can take the mean among levels on the columns as well:

data_mean.mean(axis=1, level='type') # row average over the year 

panel data is fundamentally a dense data representation, while multi-indexing is fundamentally a sparse data representation. As the number of dimensions increases, the dense representation can become very inefficient for the majority of real-world datasets.

Combining Datasets: Concat and Append#

TOC

Recall: Concatenation of NumPy Arrays
Simple Concatenation with pd.concat
- Duplicate indices
  - Catching the repeats as an error
  - Ignoring the index
  - Adding MultiIndex keys
- Concatenation with joins
- The append() method

By default, the concatenation takes place row-wise within the DataFrame (i.e., axis=0/’row’ or stack). Like np.concatenate, pd.concat allows specification of an axis along which concatenation will take place.
One important difference between np.concatenate and pd.concat is that Pandas concatenation preserves indices, even if the result will have duplicate indices! While this is valid within DataFrames, the outcome is often undesirable. pd.concat() gives us a few ways to handle it. (i.e. next bullet point)
If you’d like to simply verify that the indices in the result of pd.concat() do not overlap, you can specify the verify_integrity flag. With this set to True, the concatenation will raise an exception if there are duplicate indices.
Because direct array concatenation is so common, Series and DataFrame objects have an append method that can accomplish the same thing in fewer keystrokes: df1.append(df2)
- Keep in mind that unlike the append() and extend() methods of Python lists, the append() method in Pandas does not modify the original object–instead it creates a new object with the combined data. Thus, if you plan to do multiple append operations, it is generally better to build a list of DataFrames and pass them all at once to the concat() function.

Combining Datasets: Merge and Join#

TOC

Relational Algebra
- The behavior implemented in pd.merge() is a subset of what is known as relational algebra, which is a formal set of rules for manipulating relational data, and forms the conceptual foundation of operations available in most databases.
- The strength of the relational algebra approach is that it proposes several primitive operations, which become the building blocks of more complicated operations on any dataset. With this lexicon of fundamental operations implemented efficiently in a database or other program, a wide range of fairly complicated composite operations can be performed.
Categories of Joins
- The pd.merge() function implements a number of types of joins: the one-to-one, many-to-one, and many-to-many joins. All three types of joins are accessed via an identical call to the pd.merge() interface; the type of join performed depends on the form of the input data.
- One-to-one joins
  - keep in mind that the merge in general discards the index, except in the special case of merges by index (see the left_index and right_index keywords)
- Many-to-one joins
- Many-to-many joins
Specification of the Merge Key
- The on keyword
- The left_on and right_on keywords
  - At times you may wish to merge two datasets with different column names; for example, we may have a dataset in which the employee name is labeled as “name” rather than “employee”. In this case, we can use the left_on and right_on keywords to specify the two column names
```
pd.merge(df1, df3, left_on="employee", right_on="name").drop('name', axis=1)
```
- The left_index and right_index keywords
  - For convenience, DataFrames implement the join() method, which performs a merge that defaults to joining on indices
```
df1a.join(df2a)
```
  - If you’d like to mix indices and columns, you can combine left_index with right_on or left_on with right_index to get the desired behavior
```
pd.merge(df1a, df3, left_index=True, right_on='name')
```
Specifying Set Arithmetic for Joins
- We can specify this explicitly using the how keyword, which defaults to “inner”
- Other options for the how keyword are ‘outer’, ‘left’, and ‘right’
Overlapping Column Names: The suffixes Keyword
- In a case where your two input DataFrames have conflicting column names, it is possible to specify a custom suffix using the suffixes keyword
```
pd.merge(df8, df9, on="name", suffixes=["_L", "_R"])
```

Aggregation and Grouping#

TOC

Planets Data
Simple Aggregation in Pandas
- For a DataFrame, by default the aggregates (i.e. compute the summary statistics) return results within each column
- There is a convenience method describe() that computes several common aggregates for each column and returns the result.
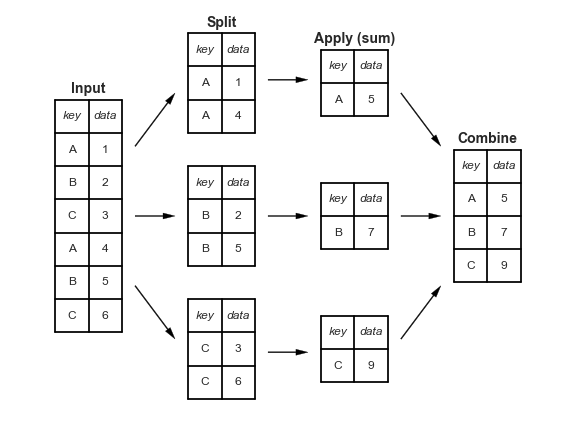
GroupBy: Split, Apply, Combine
This makes clear what the groupby accomplishes:
```
- The *split* step involves breaking up and grouping a DataFrame depending on the value of the specified key.
- The *apply* step involves computing some function, usually an aggregate, transformation, or filtering, within the individual groups.
- The *combine* step merges the results of these operations into an output array.
```
- While this could certainly be done manually using some combination of the masking, aggregation, and merging commands covered earlier, an important realization is that the intermediate splits do not need to be explicitly instantiated. Rather, the GroupBy can (often) do this in a single pass over the data, updating the sum, mean, count, min, or other aggregate for each group along the way. The power of the GroupBy is that it abstracts away these steps: the user need not think about how the computation is done under the hood, but rather thinks about the operation as a whole.
- The name “group by” comes from a command in the SQL database language, but it is perhaps more illuminative to think of it in the terms first coined by Hadley Wickham of Rstats fame: split, apply, combine.
- Notice that what is returned is not a set of DataFrames, but a DataFrameGroupBy object. This object is where the magic is: you can think of it as a special view of the DataFrame, which is poised to dig into the groups but does no actual computation until the aggregation is applied. This “lazy evaluation” approach means that common aggregates can be implemented very efficiently in a way that is almost transparent to the user.
- Split, apply, combine
- The GroupBy object
  - Column indexing
  - Iteration over groups
  - Dispatch methods
- Aggregate, filter, transform, apply
  - Aggregation
  - Filtering
  - Transformation
  - The apply() method
    - The apply() method lets you apply an arbitrary function to the group results. The function should take a DataFrame, and return either a Pandas object (e.g., DataFrame, Series) or a scalar; the combine operation will be tailored to the type of output returned.
    df.groupby('key').apply(norm_by_data2)
- Specifying the split key
  - A list, array, series, or index providing the grouping keys
  - A dictionary or series mapping index to group
  - Any Python function
  - A list of valid keys
Grouping example

Pivotal tables#

TOC

Motivating Pivot Tables
- The pivot table takes simple column-wise data as input, and groups the entries into a two-dimensional table that provides a multidimensional summarization of the data. The difference between pivot tables and GroupBy can sometimes cause confusion; It helpsto think of pivot tables as essentially a multidimensional version of GroupBy aggregation. That is, you split-apply-combine, but both the split and the combine happen across not a one-dimensional index, but across a two-dimensional grid.

Pivot Tables by Hand

titanic.groupby(['sex', 'class'])['survived'].aggregate('mean').unstack()

Pivot Table Syntax

titanic.pivot_table('survived', index='sex', columns='class')

Multi-level pivot tables

age = pd.cut(titanic['age'], [0, 18, 80])
titanic.pivot_table('survived', ['sex', age], 'class')

Additional pivot table options

Example: Birthrate DataFurther data exploration¶
- Further data exploration
  - You can learn more about sigma-clipping operations in a book I coauthored with Željko Ivezić, Andrew J. Connolly, and Alexander Gray: “Statistics, Data Mining, and Machine Learning in Astronomy” (Princeton University Press, 2014)

Vectorized String Operations#

TOC

Introducing Pandas String Operations
- This vectorization of operations simplifies the syntax of operating on arrays of data: we no longer have to worry about the size or shape of the array, but just about what operation we want done. For arrays of strings, NumPy does not provide such simple access, and thus you’re stuck using a more verbose loop syntax

Tables of Pandas String Methods

Methods similar to Python string methods
- Nearly all Python’s built-in string methods are mirrored by a Pandas vectorized string method. Here is a list of Pandas str methods that mirror Python string methods len() lower() translate() islower()
  ljust() upper() startswith() isupper()
  rjust() find() endswith() isnumeric()
  center() rfind() isalnum() isdecimal()
  zfill() index() isalpha() split()
  strip() rindex() isdigit() rsplit()
  rstrip() capitalize() isspace() partition()
  lstrip() swapcase() istitle() rpartition()

Methods using regular expressions

Method	Description
`match()`	Call `re.match()` on each element, returning a boolean.
`extract()`	Call `re.match()` on each element, returning matched groups as strings.
`findall()`	Call `re.findall()` on each element
`replace()`	Replace occurrences of pattern with some other string
`contains()`	Call `re.search()` on each element, returning a boolean
`count()`	Count occurrences of pattern
`split()`	Equivalent to str.split(), but accepts regexps
`rsplit()`	Equivalent to str.rsplit(), but accepts regexps

Miscellaneous methods

Method	Description
`get()`	Index each element
`slice()`	Slice each element
`slice_replace()`	Replace slice in each element with passed value
`cat()`	Concatenate strings
`repeat()`	Repeat values
`normalize()`	Return Unicode form of string
`pad()`	Add whitespace to left, right, or both sides of strings
`wrap()`	Split long strings into lines with length less than a given width
`join()`	Join strings in each element of the Series with passed separator
`get_dummies()`	extract dummy variables as a dataframe

Vectorized item access and slicing
Indicator variables

Example: Recipe Database
- A simple recipe recommender
- Going further with recipes

Working with Time Series#

TOC

Date and time data comes in a few flavors, which we will discuss here:
- Time stamps reference particular moments in time (e.g., July 4th, 2015 at 7:00am).
- Time intervals and periods reference a length of time between a particular beginning and end point; for example, the year 2015. Periods usually reference a special case of time intervals in which each interval is of uniform length and does not overlap (e.g., 24 hour-long periods comprising days).
- Time deltas or durations reference an exact length of time (e.g., a duration of 22.56 seconds).

Dates and Times in Python

Native Python dates and times: datetime and dateutil
- Python’s basic objects for working with dates and times reside in the built-in datetime module. Along with the third-party dateutil module, you can use it to quickly perform a host of useful functionalities on dates and times.
- A related package to be aware of is pytz, which contains tools for working with the most migrane-inducing piece of time series data: time zones.

Typed arrays of times: NumPy’s datetime64

The weaknesses of Python’s datetime format inspired the NumPy team to add a set of native time series data type to NumPy. The datetime64 dtype encodes dates as 64-bit integers, and thus allows arrays of dates to be represented very compactly. The datetime64 requires a very specific input format:

import numpy as np
date = np.array('2015-07-04', dtype=np.datetime64)
date
>>> array(datetime.date(2015, 7, 4), dtype='datetime64[D]')

One detail of the datetime64 and timedelta64 objects is that they are built on a fundamental time unit. Because the datetime64 object is limited to 64-bit precision, the range of encodable times is $2^{64}$ times this fundamental unit. In other words, datetime64 imposes a trade-off between time resolution and maximum time span.
The time zone is automatically set to the local time on the computer executing the code. You can force any desired fundamental unit using one of many format codes

Code	Meaning	Time span (relative)	Time span (absolute)
Y	Year	± 9.2e18 years	[9.2e18 BC, 9.2e18 AD]
M	Month	± 7.6e17 years	[7.6e17 BC, 7.6e17 AD]
W	Week	± 1.7e17 years	[1.7e17 BC, 1.7e17 AD]
D	Day	± 2.5e16 years	[2.5e16 BC, 2.5e16 AD]
h	Hour	± 1.0e15 years	[1.0e15 BC, 1.0e15 AD]
m	Minute	± 1.7e13 years	[1.7e13 BC, 1.7e13 AD]
s	Second	± 2.9e12 years	[ 2.9e9 BC, 2.9e9 AD]
ms	Millisecond	± 2.9e9 years	[ 2.9e6 BC, 2.9e6 AD]
us	Microsecond	± 2.9e6 years	[290301 BC, 294241 AD]
ns	Nanosecond	± 292 years	[ 1678 AD, 2262 AD]
ps	Picosecond	± 106 days	[ 1969 AD, 1970 AD]
fs	Femtosecond	± 2.6 hours	[ 1969 AD, 1970 AD]
as	Attosecond	± 9.2 seconds	[ 1969 AD, 1970 AD]

For the types of data we see in the real world, a useful default is datetime64[ns], as it can encode a useful range of modern dates with a suitably fine precision.
we will note that while the datetime64 data type addresses some of the deficiencies of the built-in Python datetime type, it lacks many of the convenient methods and functions provided by datetime and especially dateutil.

Dates and times in pandas: best of both worlds
- Pandas builds upon all the tools just discussed to provide a Timestamp object, which combines the ease-of-use of datetime and dateutil with the efficient storage and vectorized interface of numpy.datetime64. From a group of these Timestamp objects, Pandas can construct a DatetimeIndex that can be used to index data in a Series or DataFrame
The power of datetime and dateutil lie in their flexibility and easy syntax: you can use these objects and their built-in methods to easily perform nearly any operation you might be interested in. Where they break down is when you wish to work with large arrays of dates and times: just as lists of Python numerical variables are suboptimal compared to NumPy-style typed numerical arrays, lists of Python datetime objects are suboptimal compared to typed arrays of encoded dates.

Pandas Time Series: Indexing by Time
- Where the Pandas time series tools really become useful is when you begin to index data by timestamps.
Pandas Time Series Data Structures
- For time stamps, Pandas provides the Timestamp type. The associated Index structure is DatetimeIndex.
- For time Periods, Pandas provides the Period type. This encodes a fixed-frequency interval based on numpy.datetime64. The associated index structure is PeriodIndex.
- For time deltas or durations, Pandas provides the Timedelta type. Timedelta is a more efficient replacement for Python’s native datetime.timedelta type, and is based on numpy.timedelta64. The associated index structure is TimedeltaIndex.
- The most fundamental of these date/time objects are the Timestamp and DatetimeIndex objects. While these class objects can be invoked directly, it is more common to use the pd.to_datetime() function, which can parse a wide variety of formats. Passing a single date to pd.to_datetime() yields a Timestamp; passing a series of dates by default yields a DatetimeIndex
```
dates = pd.to_datetime([datetime(2015, 7, 3), '4th of July, 2015',
                 '2015-Jul-6', '07-07-2015', '20150708'])
dates
>>> DatetimeIndex(['2015-07-03', '2015-07-04', '2015-07-06', '2015-07-07',
         '2015-07-08'],
        dtype='datetime64[ns]', freq=None)
```
- A TimedeltaIndex is created, for example, when a date is subtracted from another:
```
dates - dates[0]
>>> TimedeltaIndex(['0 days', '1 days', '3 days', '4 days', '5 days'], dtype='timedelta64[ns]', freq=None)
```
- Regular sequences: pd.date_range()

Frequencies and Offsets

Fundamental to these Pandas time series tools is the concept of a frequency or date offset.

Code	Description	Code	Description
D	Calendar day	B	Business day
W	Weekly
M	Month end	BM	Business month end
Q	Quarter end	BQ	Business quarter end
A	Year end	BA	Business year end
H	Hours	BH	Business hours
T	Minutes
S	Seconds
L	Milliseonds
U	Microseconds
N	nanoseconds

The monthly, quarterly, and annual frequencies are all marked at the end of the specified period. By adding an S suffix to any of these, they instead will be marked at the beginning:

Code	Description	Code	Description
MS	Month start	BMS	Business month start
QS	Quarter start	BQS	Business quarter start
AS	Year start	BAS	Business year start

Resampling, Shifting, and Windowing
- Resampling and converting frequencies
  - One common need for time series data is resampling at a higher or lower frequency. This can be done using the resample() method, or the much simpler asfreq() method. The primary difference between the two is that resample() is fundamentally a data aggregation, while asfreq() is fundamentally a data selection.
- Time-shifts
- Rolling windows
Where to Learn More
Example: Visualizing Seattle Bicycle Counts
- Visualizing the data
- Digging into the data

High-Performance Pandas: eval() and query()#

TOC

As of version 0.13 (released January 2014), Pandas includes some experimental tools that allow you to directly access C-speed operations without costly allocation of intermediate arrays. These are the eval() and query() functions, which rely on the Numexpr package.
Motivating query() and eval(): Compound Expressions
- In other words, every intermediate step is explicitly allocated in memory. If the x and y arrays are very large, this can lead to significant memory and computational overhead. The Numexpr library gives you the ability to compute this type of compound expression element by element, without the need to allocate full intermediate arrays.
- The benefit here is that Numexpr evaluates the expression in a way that does not use full-sized temporary arrays, and thus can be much more efficient than NumPy, especially for large arrays. The Pandas eval() and query() tools that we will discuss here are conceptually similar, and depend on the Numexpr package.
pandas.eval() for Efficient Operations
- The eval() function in Pandas uses string expressions to efficiently compute operations using DataFrames
```
pd.eval('df1 + df2 + df3 + df4')
```
- Operations supported by pd.eval()
  - Comparison operators
  - Bitwise operators
  - Object attributes and indices
  - Other operations
DataFrame.eval() for Column-Wise Operations
- Just as Pandas has a top-level pd.eval() function, DataFrames have an eval() method that works in similar ways. The benefit of the eval() method is that columns can be referred to by name:
```
pd.eval("(df.A + df.B) / (df.C - 1)")
```
- Assignment in DataFrame.eval()
  - In addition to the options just discussed, DataFrame.eval() also allows assignment to any column.
    df.eval('D = (A - B) / C', inplace=True) # compute D based on A, B, and C
- Local variables in DataFrame.eval()
  - The DataFrame.eval() method supports an additional syntax that lets it work with local Python variables.
  - The @ character here marks a variable name rather than a column name, and lets you efficiently evaluate expressions involving the two “namespaces”: the namespace of columns, and the namespace of Python objects. Notice that this @ character is only supported by the DataFrame.eval() method, not by the pandas.eval() function, because the pandas.eval() function only has access to the one (Python) namespace.

DataFrame.query() Method

Note that the query() method also accepts the @ flag to mark local variables

Cmean = df['C'].mean()
result1 = df[(df.A < Cmean) & (df.B < Cmean)]
result2 = df.query('A < @Cmean and B < @Cmean')
np.allclose(result1, result2)

Performance: When to Use These Functions
- When considering whether to use these functions, there are two considerations: computation time and memory use. Memory use is the most predictable aspect. As already mentioned, every compound expression involving NumPy arrays or Pandas DataFrames will result in implicit creation of temporary arrays
- If the size of the temporary DataFrames is significant compared to your available system memory (typically several gigabytes) then it’s a good idea to use an eval() or query() expression.
- On the performance side, eval() can be faster even when you are not maxing-out your system memory. The issue is how your temporary DataFrames compare to the size of the L1 or L2 CPU cache on your system (typically a few megabytes in 2016); if they are much bigger, then eval() can avoid some potentially slow movement of values between the different memory caches. In practice, I find that the difference in computation time between the traditional methods and the eval/query method is usually not significant–if anything, the traditional method is faster for smaller arrays! The benefit of eval/query is mainly in the saved memory, and the sometimes cleaner syntax they offer.

Further Resources#

3. Machine Learning :computer:#

What Is Machine Learning?#

The study of machine learning certainly arose from research in this context, but in the data science application of machine learning methods, it’s more helpful to think of machine learning as a means of building models of data.
Fundamentally, machine learning involves building mathematical models to help understand data. “Learning” enters the fray when we give these models tunable parameters that can be adapted to observed data; in this way the program can be considered to be “learning” from the data. Once these models have been fit to previously seen data, they can be used to predict and understand aspects of newly observed data.
Categories of Machine Learning
- Supervised learning involves somehow modeling the relationship between measured features of data and some label associated with the data; once this model is determined, it can be used to apply labels to new, unknown data.
  - Classification
  - Regression
- Unsupervised learning involves modeling the features of a dataset without reference to any label, and is often described as “letting the dataset speak for itself.”
  - Clustering
  - Dimensionality reduction
- In addition, there are so-called semi-supervised learning methods, which falls somewhere between supervised learning and unsupervised learning. Semi-supervised learning methods are often useful when only incomplete labels are available.
Qualitative Examples of Machine Learning Applications
- Classification: Predicting discrete labels
- Regression: Predicting continuous labels
- Clustering: Inferring labels on unlabeled data
- Dimensionality reduction: Inferring structure of unlabeled data
Summary

Introducing Scikit-Learn#

TOC

Data Representation in Scikit-Learn
- The best way to think about data within Scikit-Learn is in terms of tables of data.
- Data as table
  - Features matrix
  - Target array
    - Often one point of confusion is how the target array differs from the other features columns. The distinguishing feature of the target array is that it is usually the quantity we want to predict from the data: in statistical terms, it is the dependent variable.
Scikit-Learn’s Estimator API
- The Scikit-Learn API is designed with the following guiding principles in mind, as outlined in the Scikit-Learn API paper:
  - Consistency: All objects share a common interface drawn from a limited set of methods, with consistent documentation.
  - Inspection: All specified parameter values are exposed as public attributes.
  - Limited object hierarchy: Only algorithms are represented by Python classes; datasets are represented in standard formats (NumPy arrays, Pandas DataFrames, SciPy sparse matrices) and parameter names use standard Python strings.
  - Composition: Many machine learning tasks can be expressed as sequences of more fundamental algorithms, and Scikit-Learn makes use of this wherever possible.
  - Sensible defaults: When models require user-specified parameters, the library defines an appropriate default value.
- In practice, these principles make Scikit-Learn very easy to use, once the basic principles are understood. Every machine learning algorithm in Scikit-Learn is implemented via the Estimator API, which provides a consistent interface for a wide range of machine learning applications.
- Basics of the API
  - Most commonly, the steps in using the Scikit-Learn estimator API are as follows (we will step through a handful of detailed examples in the sections that follow).
    1. Choose a class of model by importing the appropriate estimator class from Scikit-Learn.
    2. Choose model hyperparameters by instantiating this class with desired values.
    3. Arrange data into a features matrix and target vector following the discussion above.
    4. Fit the model to your data by calling the fit() method of the model instance.
    5. Apply the Model to new data:
      - For supervised learning, often we predict labels for unknown data using the predict() method.
      - For unsupervised learning, we often transform or infer properties of the data using the transform() or predict() method.
- Supervised learning example: Simple linear regression
  1. Choose a class of model
  2. Choose model hyperparameters
    - An important point is that a class of model is not the same as an instance of a model.
    - In Scikit-Learn, by convention all model parameters that were learned during the fit() process have trailing underscores
    - Keep in mind that when the model is instantiated, the only action is the storing of these hyperparameter values. In particular, we have not yet applied the model to any data: the Scikit-Learn API makes very clear the distinction between choice of model and application of model to data.
  3. Arrange data into a features matrix and target vector
    - In general, Scikit-Learn does not provide tools to draw conclusions from internal model parameters themselves: interpreting model parameters is much more a statistical modeling question than a machine learning question.
  4. Fit the model to your data
  5. Predict labels for unknown data
- Supervised learning example: Iris classification
  - Because it is so fast and has no hyperparameters to choose, Gaussian naive Bayes is often a good model to use as a baseline classification, before exploring whether improvements can be found through more sophisticated models.
- Unsupervised learning example: Iris dimensionality
  - Often dimensionality reduction is used as an aid to visualizing data: after all, it is much easier to plot data in two dimensions than in four dimensions or higher!
- Unsupervised learning: Iris clustering
Application: Exploring Hand-written Digits
- Loading and visualizing the digits data
- Unsupervised learning: Dimensionality reduction
- Classification on digits
Summary

Hyperparameters and Model Validation#

TOC

Thinking about Model Validation
- Model validation the wrong way
- Model validation the right way: Holdout sets
- Model validation via cross-validation
  - One disadvantage of using a holdout set for model validation is that we have lost a portion of our data to the model training.
  - One way to address this is to use cross-validation; that is, to do a sequence of fits where each subset of the data is used both as a training set and as a validation set.
  - Scikit-Learn implements a number of useful cross-validation schemes that are useful in particular situations; these are implemented via iterators in the cross_validation module.
Selecting the Best Model
- Of core importance is the following question: if our estimator is underperforming, how should we move forward? There are several possible answers:
  - Use a more complicated/more flexible model
  - Use a less complicated/less flexible model
  - Gather more training samples
  - Gather more data to add features to each sample
- The answer to this question is often counter-intuitive. In particular, sometimes using a more complicated model will give worse results, and adding more training samples may not improve your results! The ability to determine what steps will improve your model is what separates the successful machine learning practitioners from the unsuccessful.
- The Bias-variance trade-off
  - For high-bias models, the performance of the model on the validation set is similar to the performance on the training set.
  - For high-variance models, the performance of the model on the validation set is far worse than the performance on the training set.
- Validation curves in Scikit-Learn
Learning Curves
- We see that the behavior of the validation curve has not one but two important inputs: the model complexity and the number of training points. It is often useful to to explore the behavior of the model as a function of the number of training points, which we can do by using increasingly larger subsets of the data to fit our model. A plot of the training/validation score with respect to the size of the training set is known as a learning curve.
- One important aspect of model complexity is that the optimal model will generally depend on the size of your training data.
- The notable feature of the learning curve is the convergence to a particular score as the number of training samples grows. In particular, once you have enough points that a particular model has converged, adding more training data will not help you! The only way to increase model performance in this case is to use another (often more complex) model.
- The general behavior we would expect from a learning curve is this:
  - A model of a given complexity will overfit a small dataset: this means the training score will be relatively high, while the validation score will be relatively low.
  - A model of a given complexity will underfit a large dataset: this means that the training score will decrease, but the validation score will increase.
  - A model will never, except by chance, give a better score to the validation set than the training set: this means the curves should keep getting closer together but never cross.
- Learning curves in Scikit-Learn
  - This (learning curve) is a valuable diagnostic, because it gives us a visual depiction of how our model responds to increasing training data. In particular, when your learning curve has already converged (i.e., when the training and validation curves are already close to each other) adding more training data will not significantly improve the fit!
Validation in Practice: Grid Search
- The grid search provides many more options, including the ability to specify a custom scoring function, to parallelize the computations, to do randomized searches, and more.
Summary

Feature Engineering#

TOC

Categorical Features
- There is one clear disadvantage of this approach (one-hot encoding): if your category has many possible values, this can greatly increase the size of your dataset. However, because the encoded data contains mostly zeros, a sparse output can be a very efficient solution
- sklearn.preprocessing.OneHotEncoder and sklearn.feature_extraction.FeatureHasher are two additional tools that Scikit-Learn includes to support this type of encoding.
Text Features
- There are some issues with this approach (using Scikit-Learn’s CountVectorizer), however: the raw word counts lead to features which put too much weight on words that appear very frequently, and this can be sub-optimal in some classification algorithms. One approach to fix this is known as term frequency-inverse document frequency (TF–IDF) which weights the word counts by a measure of how often they appear in the documents
```
from sklearn.feature_extraction.text import TfidfVectorizer
vec = TfidfVectorizer()
X = vec.fit_transform(sample)
pd.DataFrame(X.toarray(), columns=vec.get_feature_names())
```
Image Features
- A comprehensive summary of feature extraction techniques for images is well beyond the scope of this section, but you can find excellent implementations of many of the standard approaches in the Scikit-Image project.
Derived Features
- This idea of improving a model not by changing the model, but by transforming the inputs, is fundamental to many of the more powerful machine learning methods.
Imputation of Missing Data

Feature Pipelines

This pipeline looks and acts like a standard Scikit-Learn object, and will apply all the specified steps to any input data.

from sklearn.pipeline import make_pipeline

model = make_pipeline(Imputer(strategy='mean'),
                  PolynomialFeatures(degree=2),
                  LinearRegression())

In Depth: Naive Bayes Classification#

TOC

Naive Bayes models are a group of extremely fast and simple classification algorithms that are often suitable for very high-dimensional datasets. Because they are so fast and have so few tunable parameters, they end up being very useful as a quick-and-dirty baseline for a classification problem.
Bayesian Classification
- This is where the “naive” in “naive Bayes” comes in: if we make very naive assumptions about the generative model for each label, we can find a rough approximation of the generative model for each class, and then proceed with the Bayesian classification.
- Different types of naive Bayes classifiers rest on different naive assumptions about the data
Gaussian Naive Bayes
- Perhaps the easiest naive Bayes classifier to understand is Gaussian naive Bayes. In this classifier, the assumption is that data from each label is drawn from a simple Gaussian distribution.
- A nice piece of this Bayesian formalism is that it naturally allows for probabilistic classification, which we can compute using the predict_proba method
- in general, the boundary in Gaussian naive Bayes is quadratic
Multinomial Naive Bayes
- The multinomial distribution describes the probability of observing counts among a number of categories, and thus multinomial naive Bayes is most appropriate for features that represent counts or count rates.
- Example: Classifying Text
When to Use Naive Bayes
- Because naive Bayesian classifiers make such stringent assumptions about data, they will generally not perform as well as a more complicated model. That said, they have several advantages:
  - They are extremely fast for both training and prediction
  - They provide straightforward probabilistic prediction
  - They are often very easily interpretable
  - They have very few (if any) tunable parameters
- Naive Bayes classifiers tend to perform especially well in one of the following situations:
  - When the naive assumptions actually match the data (very rare in practice)
  - For very well-separated categories, when model complexity is less important
  - For very high-dimensional data, when model complexity is less important

In Depth: Linear Regression#

TOC

Simple Linear Regression
Basis Function Regression
- Notice that this is still a linear model—the linearity refers to the fact that the coefficients $a_n$ never multiply or divide each other.
- Polynomial basis functions
```
from sklearn.preprocessing import PolynomialFeatures
x = np.array([2, 3, 4])
poly = PolynomialFeatures(3, include_bias=False)
poly.fit_transform(x[:, None])
```
- Gaussian basis functions
  - one useful pattern is to fit a model that is not a sum of polynomial bases, but a sum of Gaussian bases. (add pic here)
  - This is typical over-fitting behavior when basis functions overlap: the coefficients of adjacent basis functions blow up and cancel each other out.
Regularization
- Ridge regression ($L_2$ Regularization)
  - Perhaps the most common form of regularization is known as ridge regression or $L_2$ regularization, sometimes also called Tikhonov regularization. This proceeds by penalizing the sum of squares (2-norms) of the model coefficients; in this case, the penalty on the model fit would be $$P = \alpha\sum_{n=1}^N \theta_n^2$$ where $\alpha$ is a free parameter that controls the strength of the penalty.
    from sklearn.linear_model import Ridge model = make_pipeline(GaussianFeatures(30), Ridge(alpha=0.1)) basis_plot(model, title='Ridge Regression')
- Lasso regression ($L_1$ regularization)
  - Another very common type of regularization is known as lasso, and involves penalizing the sum of absolute values (1-norms) of regression coefficients: $$P = \alpha\sum_{n=1}^N|\theta_n|$$
  - due to geometric reasons lasso regression tends to favor sparse models where possible: that is, it preferentially sets model coefficients to exactly zero.
```
from sklearn.linear_model import Lasso
model = make_pipeline(GaussianFeatures(30), Lasso(alpha=0.001))
basis_plot(model, title='Lasso Regression')
```
Example: Predicting Bicycle Traffic

In-Depth: Support Vector Machines#

TOC

Motivating Support Vector Machines
- Generative classification: when learning a simple model describing the distribution of each underlying class, and uses these generative models to probabilistically determine labels for new points .
- In SVM we consider discriminative classification: rather than modeling each class, we simply find a line or curve (in two dimensions) or manifold (in multiple dimensions) that divides the classes from each other.
Support Vector Machines: Maximizing the Margin
- Support vector machines offer one way to improve on this. The intuition is this: rather than simply drawing a zero-width line between the classes, we can draw around each line a margin of some width, up to the nearest point.
- In support vector machines, the line that maximizes this margin is the one we will choose as the optimal model. Support vector machines are an example of such a maximum margin estimator.
- Fitting a support vector machine
```
from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1E10)
model.fit(X, y)
```
  - A key to this classifier’s success is that for the fit, only the position of the support vectors matter; any points further from the margin which are on the correct side do not modify the fit! Technically, this is because these points do not contribute to the loss function used to fit the model, so their position and number do not matter so long as they do not cross the margin.
- Beyond linear boundaries: Kernel SVM
  - Idea: when linear separation is not possible, project the data into a higher dimension such that a linear separator would be sufficient.
  - One strategy to this end is to compute a basis function centered at every point in the dataset, and let the SVM algorithm sift through the results. This type of basis function transformation is known as a kernel transformation, as it is based on a similarity relationship (or kernel) between each pair of points.
  - A potential problem with this strategy—projecting $N$ points into $N$ dimensions—is that it might become very computationally intensive as $N$ grows large. However, because of a neat little procedure known as the kernel trick, a fit on kernel-transformed data can be done implicitly—that is, without ever building the full $N$-dimensional representation of the kernel projection! This kernel trick is built into the SVM, and is one of the reasons the method is so powerful.
  - In Scikit-Learn, we can apply kernelized SVM simply by changing our linear kernel to an RBF (radial basis function) kernel, using the kernel model hyperparameter:
```
clf = SVC(kernel='rbf', C=1E6)
clf.fit(X, y)
```
- Tuning the SVM: Softening Margins
  - the SVM implementation has a bit of a fudge-factor which “softens” the margin: that is, it allows some of the points to creep into the margin if that allows a better fit.
  - The hardness of the margin is controlled by a tuning parameter, most often known as $C$. For very large $C$, the margin is hard, and points cannot lie in it. For smaller $C$, the margin is softer, and can grow to encompass some points.
Example: Face Recognition
Support Vector Machine Summary
- Pros:
  - Their dependence on relatively few support vectors means that they are very compact models, and take up very little memory.
  - Once the model is trained, the prediction phase is very fast.
  - Because they are affected only by points near the margin, they work well with high-dimensional data—even data with more dimensions than samples, which is a challenging regime for other algorithms.
  - Their integration with kernel methods makes them very versatile, able to adapt to many types of data.
- Cons:
  - The scaling with the number of samples $N$ is $\mathcal{O}[N^3]$ at worst, or $\mathcal{O}[N^2]$ for efficient implementations. For large numbers of training samples, this computational cost can be prohibitive.
  - The results are strongly dependent on a suitable choice for the softening parameter $C$. This must be carefully chosen via cross-validation, which can be expensive as datasets grow in size.
  - The results do not have a direct probabilistic interpretation. This can be estimated via an internal cross-validation (see the probability parameter of SVC), but this extra estimation is costly.

In-Depth: Decision Trees and Random Forests#

TOC

Random forests are an example of an ensemble method, meaning that it relies on aggregating the results of an ensemble of simpler estimators. The somewhat surprising result with such ensemble methods is that the sum can be greater than the parts: that is, a majority vote among a number of estimators can end up being better than any of the individual estimators doing the voting!
Motivating Random Forests: Decision Trees
- In machine learning implementations of decision trees, the questions generally take the form of axis-aligned splits in the data: that is, each node in the tree splits the data into two groups using a cutoff value within one of the features.
- Creating a decision tree
```
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier().fit(X, y)
```
- Decision trees and over-fitting
  - Over-fitting turns out to be a general property of decision trees: it is very easy to go too deep in the tree, and thus to fit details of the particular data rather than the overall properties of the distributions they are drawn from.
Ensembles of Estimators: Random Forests
- Bagging makes use of an ensemble (a grab bag, perhaps) of parallel estimators, each of which over-fits the data, and averages the results to find a better classification. An ensemble of randomized decision trees is known as a random forest.
```
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(n_estimators=100, random_state=0)
```

Random Forest Regression

from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(200)
forest.fit(x, y)

Example: Random Forest for Classifying Digits
Summary of Random Forests
- Pros
  - Both training and prediction are very fast, because of the simplicity of the underlying decision trees. In addition, both tasks can be straightforwardly parallelized, because the individual trees are entirely independent entities.
  - The multiple trees allow for a probabilistic classification: a majority vote among estimators gives an estimate of the probability (accessed in Scikit-Learn with the predict_proba() method).
  - The nonparametric model is extremely flexible, and can thus perform well on tasks that are under-fit by other estimators.

In Depth: Principal Component Analysis#

TOC

Introducing Principal Component Analysis
- PCA is fundamentally a dimensionality reduction algorithm, but it can also be useful as a tool for visualization, for noise filtering, for feature extraction and engineering, and much more.
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
```
  - The projection of each data point onto the principal axes are the “principal components” of the data. This transformation from data axes to principal axes is an affine transformation, which basically means it is composed of a translation, rotation, and uniform scaling.
- PCA as dimensionality reduction
  - Using PCA for dimensionality reduction involves zeroing out one or more of the smallest principal components, resulting in a lower-dimensional projection of the data that preserves the maximal data variance.
- PCA for visualization: Hand-written digits
- What do the components mean?
  - This meaning can be understood in terms of combinations of basis vectors.
- Choosing the number of components
  - This can be determined by looking at the cumulative explained variance ratio as a function of the number of components:
    pca = PCA().fit(digits.data) plt.plot(np.cumsum(pca.explained_variance_ratio_)) plt.xlabel('number of components') plt.ylabel('cumulative explained variance');
PCA as Noise Filtering
- The idea is this: any components with variance much larger than the effect of the noise should be relatively unaffected by the noise. So if you reconstruct the data using just the largest subset of principal components, you should be preferentially keeping the signal and throwing out the noise.
Example: Eigenfaces
Principal Component Analysis Summary
- Cons:
  - PCA’s main weakness is that it tends to be highly affected by outliers in the data.
  - While PCA is flexible, fast, and easily interpretable, it does not perform so well when there are nonlinear relationships within the data
  - For this reason, many robust variants of PCA have been developed, many of which act to iteratively discard data points that are poorly described by the initial components. Scikit-Learn contains a couple interesting variants on PCA, including RandomizedPCA and SparsePCA, both also in the sklearn.decomposition submodule.

In-Depth: Manifold Learning#

TOC

Here we will demonstrate a number of manifold methods, going most deeply into a couple techniques: multidimensional scaling (MDS), locally linear embedding (LLE), and isometric mapping (IsoMap).
manifold learning—a class of unsupervised estimators that seeks to describe datasets as low-dimensional manifolds embedded in high-dimensional spaces.
Manifold learning algorithms would seek to learn about the fundamental two-dimensional nature of the paper, even as it is contorted to fill the three-dimensional space.
Manifold learning algorithms would seek to learn about the fundamental two-dimensional nature of the paper, even as it is contorted to fill the three-dimensional space.
Manifold Learning: “HELLO”
Multidimensional Scaling (MDS)
- What the multidimensional scaling algorithm aims to do: given a distance matrix between points, it recovers a $D$-dimensional coordinate representation of the data.
MDS as Manifold Learning
- The goal of a manifold learning estimator: given high-dimensional embedded data, it seeks a low-dimensional representation of the data that preserves certain relationships within the data. In the case of MDS, the quantity preserved is the distance between every pair of points.
Nonlinear Embeddings: Where MDS Fails
- Where MDS breaks down is when the embedding is nonlinear—that is, when it goes beyond this simple set of operations.
- linear embeddings, which essentially consist of rotations, translations, and scalings of data into higher-dimensional spaces.
Nonlinear Manifolds: Locally Linear Embedding
- locally linear embedding (LLE): rather than preserving all distances, it instead tries to preserve only the distances between neighboring points: in this case, the nearest 100 neighbors of each point.
- Locally Linear Embedding (LLE) comes in a number of flavors; here we will use the modified LLE algorithm to recover the embedded two-dimensional manifold. In general, modified LLE does better than other flavors of the algorithm at recovering well-defined manifolds with very little distortion:
Some Thoughts on Manifold Methods
- The following are some of the particular challenges of manifold learning, which all contrast poorly with PCA:
  - In manifold learning, there is no good framework for handling missing data. In contrast, there are straightforward iterative approaches for missing data in PCA.
  - In manifold learning, the presence of noise in the data can “short-circuit” the manifold and drastically change the embedding. In contrast, PCA naturally filters noise from the most important components.
  - The manifold embedding result is generally highly dependent on the number of neighbors chosen, and there is generally no solid quantitative way to choose an optimal number of neighbors. In contrast, PCA does not involve such a choice.
  - In manifold learning, the globally optimal number of output dimensions is difficult to determine. In contrast, PCA lets you find the output dimension based on the explained variance.
  - In manifold learning, the meaning of the embedded dimensions is not always clear. In PCA, the principal components have a very clear meaning.
  - In manifold learning the computational expense of manifold methods scales as $O[N^2]$ or $O[N^3]$. For PCA, there exist randomized approaches that are generally much faster (though see the megaman package for some more scalable implementations of manifold learning).
- the only clear advantage of manifold learning methods over PCA is their ability to preserve nonlinear relationships in the data; for that reason I tend to explore data with manifold methods only after first exploring them with PCA.
- Scikit-Learn implements several common variants of manifold learning beyond Isomap and LLE: the Scikit-Learn documentation has a nice discussion and comparison of them.
  - For toy problems such as the S-curve we saw before, locally linear embedding (LLE) and its variants (especially modified LLE), perform very well. This is implemented in sklearn.manifold.LocallyLinearEmbedding.
  - For high-dimensional data from real-world sources, LLE often produces poor results, and isometric mapping (IsoMap) seems to generally lead to more meaningful embeddings. This is implemented in sklearn.manifold.Isomap
  - For data that is highly clustered, t-distributed stochastic neighbor embedding (t-SNE) seems to work very well, though can be very slow compared to other methods. This is implemented in sklearn.manifold.TSNE.
Example: Isomap on Faces
- One place manifold learning is often used is in understanding the relationship between high-dimensional data points. A common case of high-dimensional data is images
- We see that for this data, nearly 100 components are required to preserve 90% of the variance: this tells us that the data is intrinsically very high dimensional—it can’t be described linearly with just a few components.
Example: Visualizing Structure in Digits
- Now, this in itself may not be useful for the task of classifying digits, but it does help us get an understanding of the data, and may give us ideas about how to move forward, such as how we might want to preprocess the data before building a classification pipeline.

In Depth: k-Means Clustering#

TOC

Introducing k-Means
- The k-means algorithm searches for a pre-determined number of clusters within an unlabeled multidimensional dataset. It accomplishes this using a simple conception of what the optimal clustering looks like:
  - The “cluster center” is the arithmetic mean of all the points belonging to the cluster.
  - Each point is closer to its own cluster center than to other cluster centers.
k-Means Algorithm: Expectation–Maximization
- In short, the expectation–maximization approach here consists of the following procedure:
  1. Guess some cluster centers
  2. Repeat until converged
    1. E-Step: assign points to the nearest cluster center
    2. M-Step: set the cluster centers to the mean
  - Here the “E-step” or “Expectation step” is so-named because it involves updating our expectation of which cluster each point belongs to. The “M-step” or “Maximization step” is so-named because it involves maximizing some fitness function that defines the location of the cluster centers—in this case, that maximization is accomplished by taking a simple mean of the data in each cluster.
- Caveats of expectation–maximization
  - The globally optimal result may not be achieved
    - although the E–M procedure is guaranteed to improve the result in each step, there is no assurance that it will lead to the global best solution.
    - For this reason, it is common for the algorithm to be run for multiple starting guesses, as indeed Scikit-Learn does by default (set by the n_init parameter, which defaults to 10).
  - The number of clusters must be selected beforehand
    - Another common challenge with k-means is that you must tell it how many clusters you expect: it cannot learn the number of clusters from the data.
    - one approach that is rather intuitive, but that we won’t discuss further here, is called silhouette analysis.
    - Alternatively, you might use a more complicated clustering algorithm which has a better quantitative measure of the fitness per number of clusters (e.g., Gaussian mixture models; see In Depth: Gaussian Mixture Models) or which can choose a suitable number of clusters (e.g., DBSCAN, mean-shift, or affinity propagation, all available in the sklearn.cluster submodule)
  - k-means is limited to linear cluster boundaries
    - The fundamental model assumptions of k-means (points will be closer to their own cluster center than to others) means that the algorithm will often be ineffective if the clusters have complicated geometries.
    - the boundaries between k-means clusters will always be linear, which means that it will fail for more complicated boundaries.
    - One version of this kernelized k-means is implemented in Scikit-Learn within the SpectralClustering estimator. It uses the graph of nearest neighbors to compute a higher-dimensional representation of the data, and then assigns labels using a k-means algorithm
  - k-means can be slow for large numbers of samples
    - Because each iteration of k-means must access every point in the dataset, the algorithm can be relatively slow as the number of samples grows.
- Examples
  - Example 1: k-means on digits
- Example 2: k-means for color compression

In Depth: Gaussian Mixture Models#

TOC

In particular, the non-probabilistic nature of k-means and its use of simple distance-from-cluster-center to assign cluster membership leads to poor performance for many real-world situations.
Motivating GMM: Weaknesses of k-Means
Generalizing E–M: Gaussian Mixture Models
- A Gaussian mixture model (GMM) attempts to find a mixture of multi-dimensional Gaussian probability distributions that best model any input dataset. In the simplest case, GMMs can be used for finding clusters in the same manner as k-means
```
from sklearn.mixture import GMM
gmm = GMM(n_components=4).fit(X)
labels = gmm.predict(X)
```
- Under the hood, a Gaussian mixture model is very similar to k-means: it uses an expectation–maximization approach which qualitatively does the following:
  1. Choose starting guesses for the location and shape
  2. Repeat until converged:
    1. E-step: for each point, find weights encoding the probability of membership in each cluster
    2. M-step: for each cluster, update its location, normalization, and shape based on all data points, making use of the weights
- Choosing the covariance type
  - the covariance_type option was set differently within each. This hyperparameter controls the degrees of freedom in the shape of each cluster; it is essential to set this carefully for any given problem. The default is covariance_type="diag", which means that the size of the cluster along each dimension can be set independently, with the resulting ellipse constrained to align with the axes. A slightly simpler and faster model is covariance_type="spherical", which constrains the shape of the cluster such that all dimensions are equal. The resulting clustering will have similar characteristics to that of k-means, though it is not entirely equivalent. A more complicated and computationally expensive model (especially as the number of dimensions grows) is to use covariance_type="full", which allows each cluster to be modeled as an ellipse with arbitrary orientation.
GMM as Density Estimation
- Though GMM is often categorized as a clustering algorithm, fundamentally it is an algorithm for density estimation. That is to say, the result of a GMM fit to some data is technically not a clustering model, but a generative probabilistic model describing the distribution of the data.
- How many components?
  - The fact that GMM is a generative model gives us a natural means of determining the optimal number of components for a given dataset. A generative model is inherently a probability distribution for the dataset, and so we can simply evaluate the likelihood of the data under the model, using cross-validation to avoid over-fitting. Another means of correcting for over-fitting is to adjust the model likelihoods using some analytic criterion such as the Akaike information criterion (AIC) or the Bayesian information criterion (BIC). Scikit-Learn’s GMM estimator actually includes built-in methods that compute both of these, and so it is very easy to operate on this approach.
  - Notice the important point: this choice of number of components measures how well GMM works as a density estimator, not how well it works as a clustering algorithm. I’d encourage you to think of GMM primarily as a density estimator, and use it for clustering only when warranted within simple datasets.
Example: GMM for Generating New Data

[Van16]

Jake VanderPlas. Python data science handbook: Essential tools for working with data. " O'Reilly Media, Inc.", 2016.