Tree/Random Forest (Bagging)#
CART#
CART is binary: each node has either 2 children or 0 children
Other algorithm such as ID3 can produce decision trees with nodes have more than two children
Other types of splitting rules
oblique decision trees or binary space partition tree (BSP trees): linear split at each node
sphere trees: space is partitioned by a sphere of a certain radius around a fixed point
The CART algorithm searches for the pair of \((k, t_k)\), a feature and its cutoff point, that produces the purest subsets (weighted by their size)
CART algorithm is a greedy algorithm: it greedily searches for an optimum split at the top level, then repeats the process at each level. It does not check whether or not the split will lead to the lowest possible impurity several levels down. it is not guaranteed to be the optimal solution.
finding the optimal tree is known to be an NP-Complete problem: it requires \(O(\exp(m))\) time, making the problem intractable even for fairly small training sets.
Prediction complexity: Since each node only requires checking the value of one feature, the over all prediction complexity is just \(O(\log2(m))\), independent of the number of features
Regression tree#
If the loss function is \(l(\hat{y}, y) = (\hat{y} - y)^2\), then the best choice of score on each leaf is \(\hat{c}_m = avg(y_i|x_i \in R_m)\), where \(\{R_1, \cdots, R_M\}\) is the partition of a given tree and the final prediction of a sample is defined as
\[f(x) = \sum_{m=1}^{M} c_m I(x\in R_m)\]Assume there are \(d\) feasures \(x = (x_1, \cdots, x_d)\) and the tree is split on the \(j\)th feasure (\(j \in \{1, \cdots, d\}\)), split point \(s\in R\), then the partition based on \(j\) and \(s\):
\[R_1(j, s) = \{x|x_j\le s\}\]\[R_2(j, s) = \{x|x_j > s\}\]For each splitting variable \(x_j\) and split point \(s\),
\[\hat{c}_1(j, s) = avg(y_i|x_i\in R_1(j, s))\]\[\hat{c}_2(j, s) = avg(y_i|x_i\in R_2(j, s))\]Find \(j, s\) by minimizing loss
\[L(j,s)= \sum_{i:x_i\in R_1(j, s)}(y_i - \hat{c}_1(j, s))^2 + \sum_{i:x_i\in R_2(j, s)}(y_i - \hat{c}_2(j, s))^2\]
Overcome the potential risk of over-fitting (see regularization parameters below)
Trees can easily get over-fit if we do enough splitting
CART uses number of terminal nodes
Another option is tree depth
Complexity of a tree
Let \(|T | = M\) denote the number of terminal nodes in \(T\) , which is used to measure the complexity of a tree
Finding the optimal binary tree of a given complexity is computationally intractable
Use greedy algorithm: build the tree one node at a time, without any planning ahead
Control the complexity of a tree (i.e. avoid over-fitting)
limit max depth of tree
require all leaf nodes contain a minimum number of points
require a node have at least a certain number of data points to split
do backward pruning (the approach of CART (Breiman et al 1984)
Build a really big tree (e.g. until all regions have \(\le\) 5 points).
“Prune” the tree back greedily all the way to the root, assessing performance on validation
Classification tree#
Similar to regression, the predicted classification for node \(m\) is just the class gives the highest probability, thus the most frequent class, in that node \(m\)
\[k(m) = \text{argmax}_k\hat{p}_{mk}\]where
\[\hat{p}_{mk} = \frac{1}{N_m}\sum_{i: x_i\in R_m}I(y_i = k)\]The missclassification rate on node \(m\) is \(1 - \hat{p}_{mk(m)}\)
Loss function
0/1 loss: tractable for finding the best split but is not used usually, especially there are repeatedly splitting insteading of splitting once
Eeventually we want \(pure\) leaf node and it’s thus natrual to find splitting node and point in that node to minimizing the node impurity after splitting
Miss classification error: \(1 - \hat{p}_{mk(m)}\)
Gini index: \(\sum_{k=1}^K\hat{p}_{mk}(1-\hat{p}_{mk}) = 1 - \sum_{k=1}^K \hat{p}^2_{mk}\)
Entropy or deviance (= using information gain): \(-\sum_{k=1}^K\hat{p}_{mk}\log \hat{p}_{mk}\)
Gini and Entropy seem to be more effective, they push for more pure nodes, not just misclassification rate!
Gini impurity is slightly faster to compute, so it’s a good default. When they differe, Gini impurity tends to isolate the most frequent class in its own branch of the tree, while entropy tends to produce slightly more balanced trees.
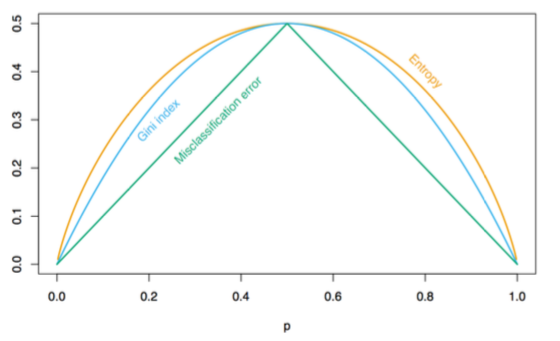
How to split
To find the split that minimize the weighted average of node impurities
\[N_L*Q(R_L) + N_R*Q(R_R)\]where \(R_L\) and \(R_R\) are potential splitting, \(N_L\) and \(N_R\) are number of observations in left and right branch after splitting and \(Q(\cdot)\) is the impurity measure
Trees in General#
Missing value in feature
Complete analysis
impute with feature mean
If categorical, set missing as a new category
Use surrogate split
For every internal node, form a list of surrogate features and split points; Goal is to approximate the original split as well as possible; Surrogates ordered by how well they approximate the original split.
Categorical feature
Suppose we have a categorical feature with \(q\) possible values (unordered).
For binary classification \(Y =\{0, 1\}\), there is an efficient algorithm
Assign each category a number, the proportion of class 0.
Then find optimal split as though it were a numeric feature.
Proved to be equivalent to search over all splits in (Breiman et al. 1984).
Trees have to work much harder to capture linear relations
Trees make no use of geometry
No inner products or distances
called a “nonmetric” method
Feature scale irrelevant
Predictions are not continuous
not so bad for classification
may not be desirable for regression
Regularization Hyperparameters: To avoid overfitting the training data, you need to restrict the Decision Tree’s freedom during training. As you know by now, this is called regularization
max_depth
min_samples_split: the minimum number of samples a node must have before it can be split
min_samples_leaf: the minimum number of samples a leaf node must have
min_weight_fraction_leaf: same as min_samples_leaf but expressed as a fraction of the total number of weighted instances
max_leaf_nodes: maximum number of leaf nodes
max_features: maximum number of features that are evaluated for splitting at each node
Instability
Decision Trees love orthogonal decision boundaries (all splits are perpendicular to an axis), which makes them sensitive to training set rotation.
One way to limit this problem is to use PCA, which often results in a better orientation of the training data.
More generally, the main issue with Decision Trees is that they are very sensitive to small variations in the training data.
Random Forests can limit this instability by averaging predictions over many trees
Tree Pruning#
Build a “big tree”
Keep splitting until every node either has zero error OR has \(C\) (e.g. 5 or 1) or fewer examples
Pruning
Consider an internal node \(n\), to prune the subtree rooted at \(n\) so that eliminate all descendents of \(n\) and \(n\) becomes a terminal node
Cost Complexity Greedy Pruning
Cost of complexity criterion with \(\alpha\):
\[C_{\alpha} = \hat{R}(T) + \alpha|T|\]where \(\hat{R}(T)\) quantifies the empirical risk and \(|T|\) is the complexity of a tree
Thus, \(C_{\alpha}\) trades off betweem empirical risk and complexity of a tree
Cost complexity pruning:
For each \(\alpha\), find the subtree \(T ⊂ T_0\) minimizing \(C_{\alpha} (T)\) (on training data).
Use cross validation to find the right choice of \(\alpha\)
We only need to try \(N_{Int}\) trees to find the final pruned tree \(T\), where \(N_{Int}\) is the number of internal nodes of \(T_0\), that is
\[\mathcal{T}= \{T_0 ⊃T_1 ⊃T_2 ⊃···⊃T_{|N_{Int}|}\}\]Those \(N_{|Int|}\) trees can be identified by repeatedly pruning the tree (remove leaf nodes of an internal node) and choosing the one that minimes \(\hat{R}(T_i) - \hat{R}(T_{i+1})\) in each step until all internal nodes are removed and just a single (leaf) node is left
Breiman et al. (1984) proved that
\[\left\{\arg\min_{T⊂T_0} C_{\alpha}(T) | \alpha \ge 0\right\} ⊂ \mathcal{T}\]
Bagging#
Parallel ensemble method \(\rightarrow\) bagging \(\rightarrow\) random forest[1]
Averaging independent prediction functions is preferred over single predictor as it reduces the variance of the prediction; however, in reality we don’t have multiple indepenent samples, instead we can use bootstrap to construct multiple samples for different predictors (bagging = bootstrap aggregation[2])
Bagging (for regression)
Draw \(B\) bootstrap samples \(D^1,...,D^B\) from original data \(D\).
Let \(\hat{f}_1, \hat{f}_2, \cdots, \hat{f}_B: \mathcal{X} \rightarrow \bf{R}\) be the prediction functions for each set
Bagged prediction function is given as
\[\hat{f}_{\text{bag}} = \frac{1}{B}\sum_{b=1}^B\hat{f}_b(x)\]\(\hat{f}_{\text{bag}}(x)\) usually has smaller variance than individual predictor \(\hat{f}_{b}(x)\)
Out-of-Bag error estimation
Each bagged predictor is trained on about 63% (e.g.) of the data. Remaining 37% are called out-of-bag (OOB) observations.
\[\hat{f}_{OOB}(x_i) = \frac{1}{S_i}\sum_{b\in S_i} \hat{f}_b(x_1)\]where \(S_i = \{b|D^b \text{does not contain ith point}\}\)
The OOB error is a good estimate of the test error.
OOB error is similar to cross validation error – both are computed on training set.
General sentiment is that bagging helps most when
Relatively unbiased base prediction functions
High variance / low stability
Bootstrap samples are
independent samples from the training set, but are not indepedendent samples from \(P_{\mathcal{X×Y}}\).
This dependence limits the amount of variance reduction we can get.
Random Forest#
Main idea of random forest
Use bagged decision trees, but modify the tree-growing procedure to reduce the correlation between trees.
Key step in random forests: When constructing each tree node, restrict choice of splitting variable to a randomly chosen subset of features of size \(m\).
Typically choose \(m \approx \sqrt{p}\), where \(p\) is the number of features.
Can choose m using cross validation.
Defining variable importance in RF#
Accuracy based importance
Permutation importance: mean decrease in classification accuracy after permuting \(X_j\) over all trees
Gini importance
Mean Gini gain produced by splitting \(X_j\) over all trees
Importance is calculated in out-of-sample trees
