Multicollinearity

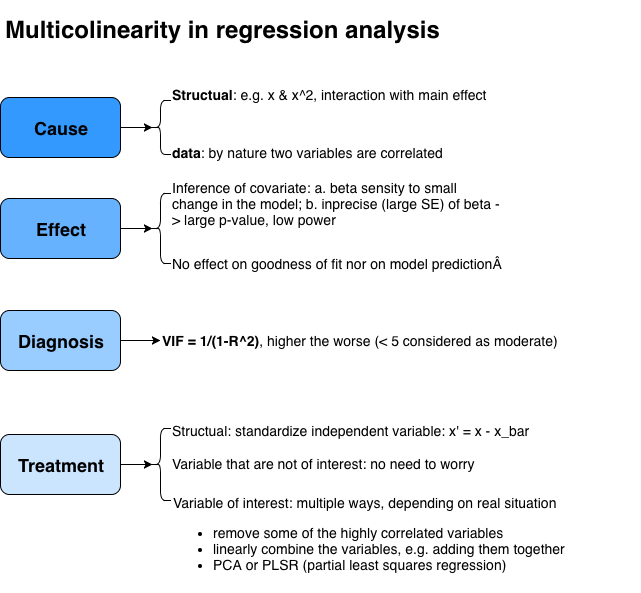
Cause

1. Structural: e.g. $x \ \&\ x^2$, interaction term and the main effect included in the interaction term
2. Data: by nature two variables are correlatd

Eeffect

• Inference of covariate
  • $\beta$ becomes sensitive to small change in the model
  • imprecise (i.e. large s.e.) of $\beta\rightarrow$ large p-value, low power
• NO effect on goodness-of-fit nor on model prediction

Diagnosis

• VIF: variance inflation factor of variable $x_i$, higher the worse (usually < 5 is moderate), is defined as:

  $$\text{VIF}_i = \frac{1}{1-R_i^2}$$

  where $R_i^2$ is the coefficient of determination when regression $X_i$ on the rest of the indepdent variables.

Treatment ​

1. Structural: standardize indepndent variable, e.g. $X' = X - \bar{X}$
2. Variables that are not of interest: no need to worry
3. Variables that are of interest:
   1. remove some of the highly correlated variables
   2. Linearly combine the variables, e.g. adding them together
   3. PCA or PLSR (partial least squares regression, ?)