Naive Bayes#

  • Naive Bayes is an algorithm used in classication, it’s one of the most ecient and eective inductive learning algorithm for machine learning.

  • In classication, the goal of a learning algorithm is to construct a classier given a set of training examples with class labels, where an example E is represented by a tuple of attribute values \((x_1, x_2,\cdots, x_n)\) and \(C\) represents the classication variable.

  • It has been observed that, however, its classication accuracy does not depend on the dependencies; i.e., naive Bayes may still have high accuracy on the datasets in which strong dependencies exist among attributes.

  • It is the distribution of de- pendencies among all attributes over classes that aects the classication of naive Bayes, not merely the dependencies themselves [Zhang, 2004]

Naive Bayes and augmented naive Bayes#

  • Classier: a function that assigns a class label to an example.

  • Bayesian classier

    The the probability of an example \(E = (x_1, x_2, \cdots, x_n)\) being class \(c\) is

    \[ p(c|E) = {{p(E|c)p(c)}\over{p(E)}} \]

    \(E\) is classified as the class \(C=+\) iff

    \[ f_b(E)= {{p(C=+|E)}\over p(C=-|E)} \ge 1 \]

    where \(f_b(E)\) is called Bayesian classifier.

  • Naive Bayesian (NB) Classier

    By assuming that all attributes are independent given the value of the class variable; that is,

    \[ p(E|c) = p(x_1, x_2, \cdots, x_n) = \prod_{i=1}^n p(x_i|c) \]

    the resulting classifier is then

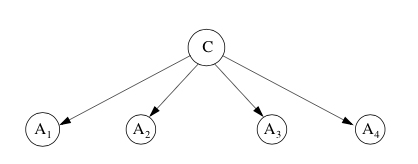
    \[ f_{nb}(E) = \frac{p(C = +)}{p(C = -)}\prod_{i=1}^n\frac{p(x_i|C=+)}{p(x_i|C=-)} \]

    Naive Bayes is the simplest form of Bayesian network, in which all attributes are independent given the value of the class variable.

    image-20211010204136545

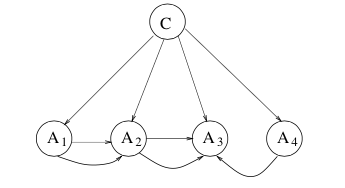
  • Augmented naive Bayes (ANB) is an extended naive Bayes, in which the class node directly points to all attribute nodes, and there exist links among attribute nodes. From the view of probability, an ANB \(G\) represents a joint probability distribution represented below.

    \[ p_G(x_1, x_2, \cdots, x_n, G) = p(c)\prod_{i=1}^np(x_i|pa(x_i), c) \]

    where \(pa(x_i)\) denotes an assignment to values of the parents of \(X_i\).

    image-20211010204424235

  • Local independence

    For each node, the inuence of its parents is quantied by the correspondent conditional probabilities. We call the dependence between a node and its parents local dependence of this node.

  • Local dependence derivative

    For a node \(X\) on ANB \(G\),the local dependence derivative of \(X\) in classes \(+\) and \(-\) are dened as

    \[\begin{split} dd_G^+(x|pa(x)) = \frac{p(x|pa(x), +)}{p(x|+)} \\ dd_G^-(x|pa(x)) = \frac{p(x|pa(x), -)}{p(x|-)} \end{split}\]

    For example, \(dd_G^+(x|pa(x))\) reflects the strength of the local dependence of node \(X\) in class \(+\), which measures the influence of \(X's\) local dependence on the classification in class \(+\).

  • Local dependence derivative ratio at node \(X\)

    For a node \(X\) on ANB \(G\),the local dependence derivative ratio at node \(X\), denoted by \(ddrG(x)\) is dened as

    \[ ddrG(x) = \frac{dd_G^+(x|pa(x))}{dd_G^-(x|pa(x))} \]

    \(ddrG(x)\) Quantifies the influence of \(X's\) local dependence on the classification.

  • Dependence distribution factor

    \[ DF_G(E) = \prod_{i=1}^n ddrG(x_i) \]
[Zha04]

Harry Zhang. The optimality of naive bayes. AA, 1(2):3, 2004.