Multiplicity in Clinical Trials#
Introduction#
Type I error rate inflated when conducting multiple hypothesis tests \((m)\) each with the nominal 0.05 significance level \((\alpha)\) –> the multiplicity problem
Source of multiplicity in clinical trials
multiple arms
control for more than one endpoint
control for more than one population
control repeatedly in time
etc.
Dealing with multiplicity
Reducing the degree of multiplicity
limit the number of questions
minimize the number of variables by using e.g. composite endpoints, summary statistic, etc.
Prioritizing questions
If multiplicity still persists
multiplicity adjustment (refer to regulatory guidance)
Common multiple test procedures#
Basic concepts#
Family-wise error rate (FWER): overall type I error rate when testing a family of null hypotheses
aim: \(Pr(\text{reject at least one true null}) \le \alpha\)
Ajusted p-values: extend ordinary (i.e. unadjusted) p-values by adjusting them for a given multiple test procedure, which can be compared directly with the significance level 𝛼, while controlling the FWER
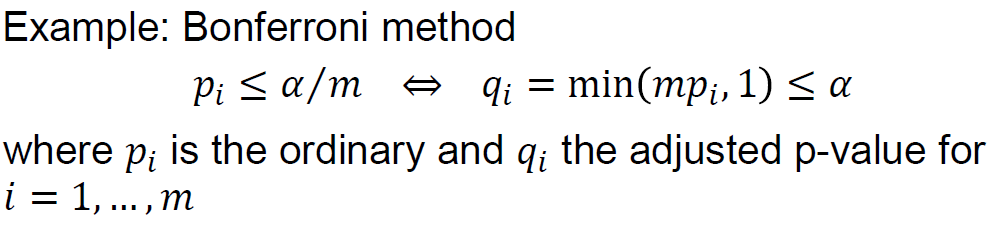
Formally, the adjusted p-value is the smallest significance level at which a given hypothesis is significant as part of the multiple test procedure. e.g.
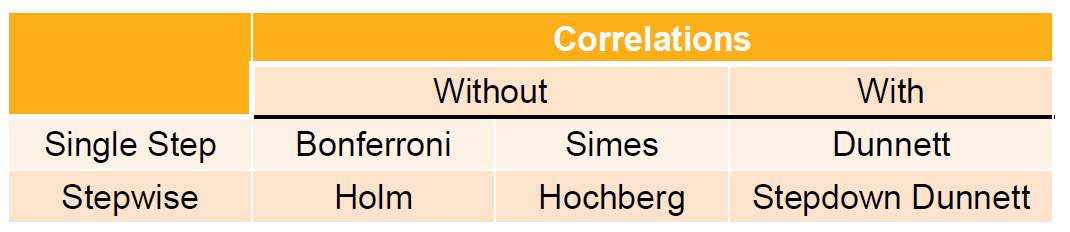
Single step methods
The rejection or non-rejection of a single hypothesis does not depend on the decision on any other hypothesis.
e.g. Bonferroni, Simes, Dunnett, etc.
Stepwise methods
The rejection or non-rejection of a particular hypothesis may depend on the decision on other hypotheses.
e.g. Holm, Hochberg, stepdown Dunnett, …
Methods#
Bonferroni#
Use 𝛼/𝑚 for all inferences; for 𝑖=1,…,𝑚: $\(\text{Reject } H_i \text{ if } p_i \le \alpha/m\)\( or with adjusted p-values \)q_i = \min(mp_i, 1)\(, \)\(\text{Reject } H_i \text{ if } q_i \le \alpha\)$
This method follows the idea of Boole’s inequality: \(Pr(\cup A_i)\le \sum_i Pr(A_i)\), where \(A_i = \{p_i\le \alpha/m\}\) denotes the event of rejecting \(H_i\)
Properties
Conservative if the number of hypotheses is large or the test statistics are strongly positively correlated
Can be improved by using stepwise methods (e.g. Holm procedure) and accounting for correlations (e.g. Dunnett test)
Rarely used in practice but is the basis for commonly used advanced procedures
Holm#
Overview
Using ordinary p-values
Using ajusted p-values
Properties
A stepwise procedure and more powerful than Bonferroni method
Sometimes called “stepdown Bonferroni” procedure
Can be improved by accounting for correlations (e.g. stepdown Dunnett test)
Simes#
Overview
Comparison with Bonferroni
Simes is more powerful than a global test based on Bonferroni
Simes assumes non-negative correlations between p-values, Bonferroni doesn’t
Hochberg (stepwise version of Simes method/stepup Simes)#
Overview
Properties
Stepup Simes
More powerful than Holm procedure
Both use same thresholds, but Hochberg starts with the largest p-value, whereas Holm starts with the smallest
It makes same assumption as the Simes test, i.e. independence or positive dependence of p-values
Can be improved, e.g. Hommel procedure based on the closed test procedure.
Dunnett#
When comparing several treatments with a control
Other methods mentioned above can also be used but only Dunnett test exploits the correlation between the p-values
Overview
linear model and hypotheses
individual test statistics
rejection rule
Properties
Single step test, which is better than Bonferroni as it exploits the known correlations between test statistics
Adjusted p-values can be calculated numerically based on the multivariate t-distribution
The Dunnett test shown here can be extended to any linear and generalized linear model
It can be improved by extending it to a stepwise procedure, similar to the Holm procedure
Other well-known parametric tests follow the same principle. For example, the Tukey test compares all treatment groups against each other, also using a multivariate -distribution
Stepwise Dunnett#
Overview
Properties
the quantiles change as hypotheses are rejected; e.g. if \(H_{(1)}\) is rejected, then the quantile \(c_{m-1, 1-\alpha}\) is computed from a (m-1)-variate t-distribution
the stepwise Dunnett test is better than the single step Dunnett test
it can be shown that \(c_{m, 1-\alpha} \ge c_{m-1, 1-\alpha}\le \cdots \le c_{1, 1-\alpha}\), where \(c_{1, 1-\alpha} = t_{v, 1-\alpha}\) is the quantile from the univariate t-distribution with \(v\) degrees of freedom
The Dunnett test uses \(c_{m, 1-\alpha}\) for all comparisons
the stepwise Dunnet test is better than the Holm procedure as it exploits the known correlations between test statistics
The stepwise version shown here is sometimes called “stepdown Dunnett” test
A “stepup Dunnett” test also exist, similar to Hochberg
Summary#
Stepwise methods are preferred over single step methods, which are less powerful and less used in practice
Accounting for correlations leads to more powerful procedures, but correlations are not always known
Simes-based methods are more powerful than Bonferroni-based methods, but control the FWER only under certain dependence structure
In practice, we select the procedure that is not only powerful from a statistical perspective, but also appropriate from clinical perspective
Hierarchical test procedure#
Background#
Previous multiple tests methods do not reflect the relative importance of the two endpoints, which is usually the case in RCT, where we have primary/secondary/exploratory endpoints with ordered importance
Previous stepwise procedures use a data-driven order of hypotheses, whereas in the RCT setting we need a multiple test procedure that specifies the order of the hypothesis based on clinical importance
Hierarchical test procedure: the hierarchy of hypotheses is specified before data is observed
Fixed sequence procedure#
Overview
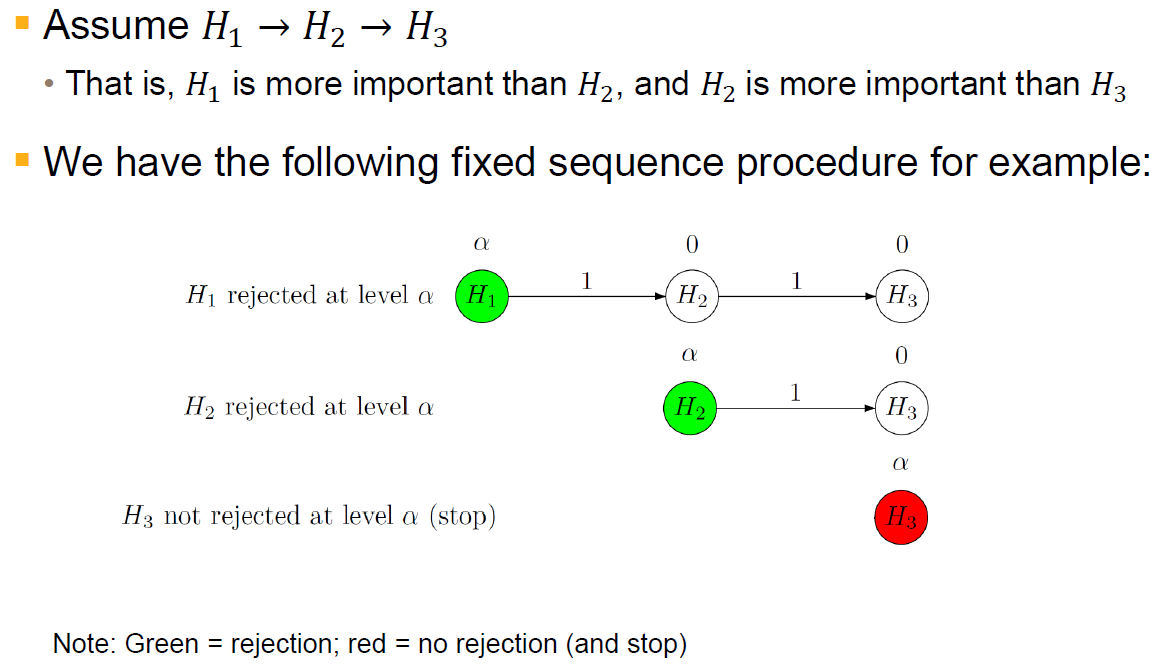
Properties
Adjusted p-values are given by \(q_i = \max\{p_1, \cdots, p_i\}, i = 1, \cdots, m\)
Advantages
Simple
Optimal when hypotheses early in the sequence are associated with large effects and performs poorly otherwise
Disadvantages
Once a hypothesis is not rejected, no further testing is permitted
Great care is advised when specifying the sequence of hypotheses
Fallback procedure#
Overview
Properties
The fixed sequence procedure is obtained as a special case from the fallback procedure by setting \(\alpha_1=\alpha\) and \(\alpha_i=0\) for \(i>1\)
In contrast to the fixed sequence procedure, fallback procedure tests all hypotheses in the pre-specified sequence even if the intitial hypotheses are not rejected
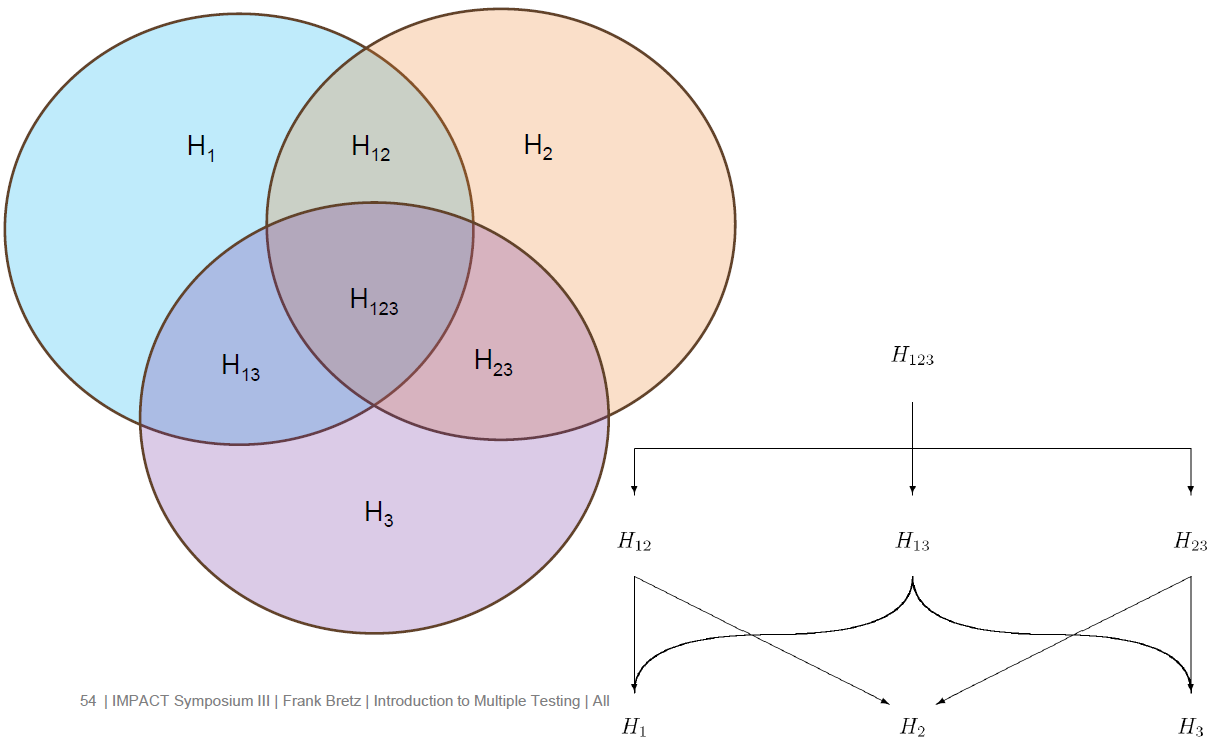
Closed test procedure (CTP)#
Overview/formal definition
Test the iteraction hypotheses using Bonferroni, Simes, Dunnett, etc. at level \(\alpha\)
Test each individual hypothesis at level \(\alpha\)
CTP using Bonferroni ( == Holm procedure)#
CTP usign Simes#
When m=2, it’s equivalent to Hochberg procedure
When m>2, it’s less powerful
CTP using Dunnett#
This is equivalent to stepdown Dunnett procedure
CTP using weighted Bonferroni#
The first is equivalent to the the fixed sequence procedure
The second version is equivalent to the fallback procedure
What if more than two hypotheses?#
Do CTP for pairwise combinations
Summary#
Summary and Conclusions#
Closed test procedure is a general principle to construct powerful multiple test procedures; many common procedures are CTPs
For structured hypotheses, one can apply the graphical approach, which is based on CTPs
It is critical to choose the suitable method for a particular problem
There are different types of multiplicity problems that need other methods than those described here, such as:
Safety data analyses
Large-scale testing in genetics, proteomics etc.
Post-hoc analyses / data snooping
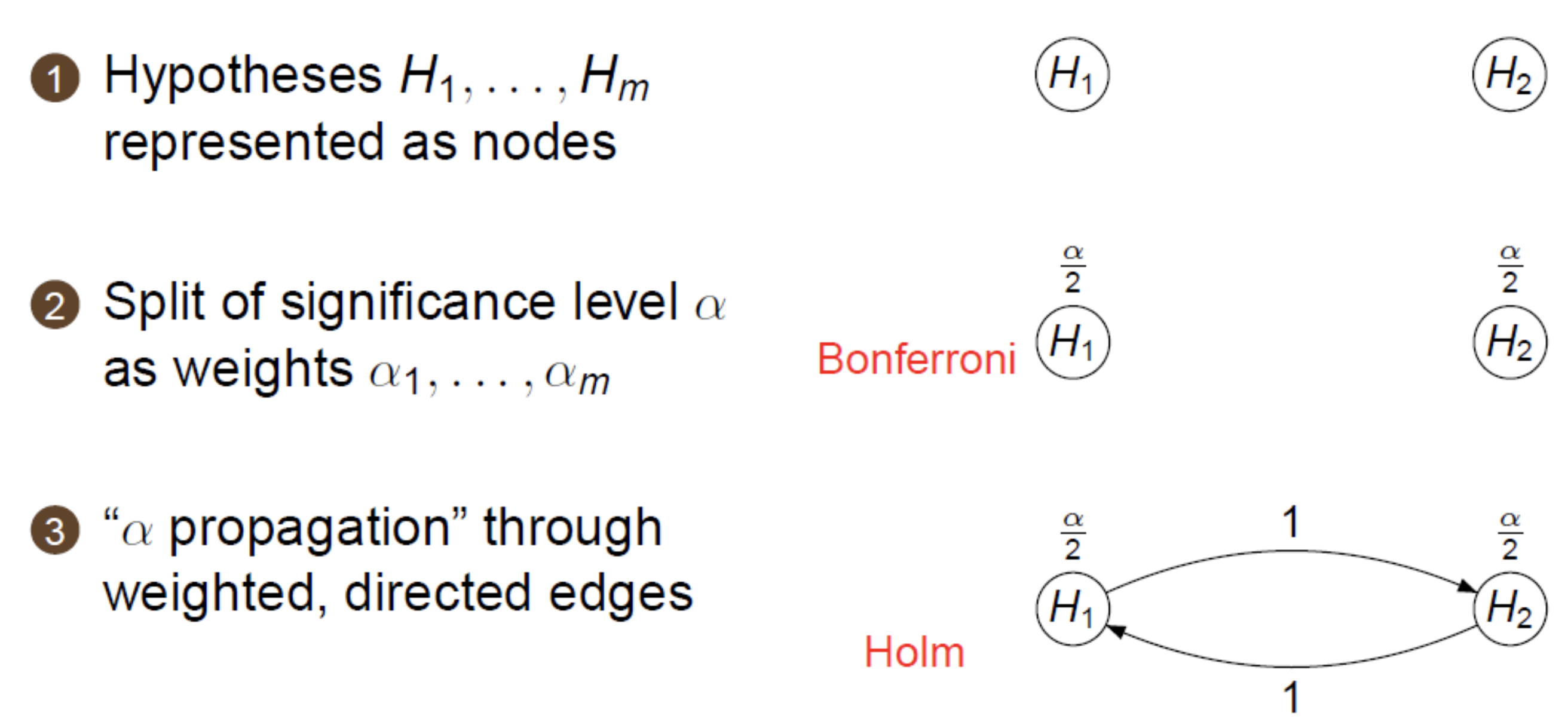
Graphical approach[Bretz et al., 2009][Bretz et al., 2011]#
Initial allocation of the significance level to \(m\) hypothesis: \(\alpha_1 + \cdots + \alpha_m = \alpha\)
\(\alpha\)-propagation: if a hypothesis \(H_i\) is rejected at level \(\alpha_i\), propagate its level \(\alpha_i\) to the remaining, not yet rejected hypotheses (according to aprefixed rule) and continue testing with the updated \(\alpha\) levels
Conventions#
Weighted Holm procedure: i.e. \(\alpha\) is no longer evenly splited among hypotheses
Common multiple test procedues#
Fixed sequence procedure
Fallback procedure
Formal description#
Initial levels \(\alpha = (\alpha_1, \cdots, \alpha_m)\) with \(\sum_{i=1}^m\alpha_i = \alpha \in (0, 1)\)
\(m \times m\) Transition matrix \(\bf{G}=(g_{ij})\), Where \(g_{ij}\) is the fraction of the level of \(H_i\) that is propagated to \(H_j\) with \(0\le g_{ij} \le 1, g_{ii} = 0\) and \(\sum_{j=1}^mg_{ij}\le1, \forall i=1, \cdots, m\)
(\(G, a\)) determine a graph with an associated multiple test
Update algorithm
The initial levels \(\alpha\), the transition matrix 𝑮, and the algorithm define a unique sequentially rejective test procedure that controls the FWER at level \(\alpha\)
Any multiple test procedure derived and visualized by a graph (\(G, \alpha\)) is based on the closed test principle
The graph (\(G, \alpha\)) and the algorithm define weighted Bonferroni tests for each intersection hypothsis in a CTP
The algorithm defines a shortcut for the resulting CTP, which does not depend on the rejection sequence
Tools:
R{gMPA} package
Summary#
Tailor advanced multiple test procedures to structured families of hypotheses
Visualize complex decision strategies in an efficient and easily communicable way
Ensure strong FWER control
It covers many common multiple test procedures as specifal cases: Holm, fixed sequence, fallback, gatekeeping, etc.
Frank Bretz, Willi Maurer, Werner Brannath, and Martin Posch. A graphical approach to sequentially rejective multiple test procedures. Statistics in medicine, 28(4):586–604, 2009.
Frank Bretz, Martin Posch, Ekkehard Glimm, Florian Klinglmueller, Willi Maurer, and Kornelius Rohmeyer. Graphical approaches for multiple comparison procedures using weighted bonferroni, simes, or parametric tests. Biometrical Journal, 53(6):894–913, 2011.