Analysis of ordinal outcome#
Analysis methods#
1. Proportional odds (PO) model#
Assumptions [1]
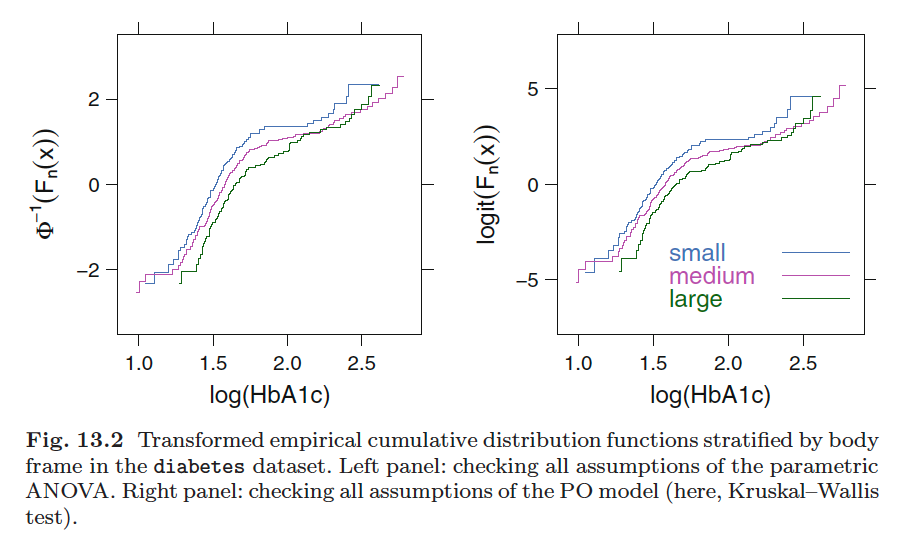
Parallelism: the logit of the CDFs of different groups should be parallel (equal distance) to each other
Check this assumption: calculated the empirical CDF(ECDF) for the response variable by group; take logit transformation of the ECDF; check for parallelism
Linearity: required ONLY if using a parametric logistic distribution instead of semi-parametric PO model
It’s semi-parametric model in the sense that it assumes additivity and linearity (by default) in formulating the probabilities but it doesn’t assume the distribution of the response variable \(Y\)
PO model assumes nothing about the actual \(Y\) distribution; it only assumes how the distribution of \(Y\) for one group is connected to the distribution of another group, i.e. the logit of the cumulative distribution functions are parallel
Connection with Wilcoxon/Kruskal-Wallis test#
PO is also what the Wilcoxon/Kruskal-Wallis test assumes to have optimal power
By treating all the distinct values in the response variable as a level, then the outcome can be seen as a ordinal variable with many categories
The hypothesis that the Wilcoxon test possess, i.e. the probability a random sample from group A is greater than a random sample from group B, is technically identical to that the general PO model tries to test (OR = 1 for any cutoff)
Numerator of the score test for the PO model, when there is only the grouping variable in the model (i.e. not adjusted), is exactly the Wilcoxon statistic
Kruskal-Wallis test can be formed using a PO model with more than one indicator variable
This can solve the transivity problem when conducting the pairwise Wilxoson tests [2]
Model (with 4 groups): \(logit[P(Y\ge y|\text{group})] = \alpha_y + \beta_1B + \beta_2C + \beta_3D\)
Advantages of PO model vs purely non-parametric counterparts#
can adjust for (continuous) covariates
more accurate p-values even with extreme number of tied values
provides a framework for consistent pairwise comparisons [2]
provides estimates of means, quantiles, and exceedance probabilities [3]
sets the sage for Bayesian PO model, so can get a Bayesian Wilcoxon test
Software#
rmspackage inRrms::orm(y ~ group)
Hmiscpackage inRPower calculation with
popowerandposamsizesimRegOrdfunction can also simulate power for an adjusted two-sample comparisonif there is one adjustment covariate
2. Check PO assumption#
Score test in
PROC LOGISTIC: extreme anti-conservatism in many casesCompare means of \(X|Y\) with and without assuming PO
Stratifying one each predictor and computing the logits of all proportions of the form \(Y\ge j, j = \text{1, 2, }\cdots, k\). When proportional odds holds, the difference in logits between different values of \(j\) should be the same at all levels of \(X\), because the model dictates that \(logit(Y\ge j| X) - logit(Y\ge i|X) = \alpha_j - \alpha_i\), for any constant \(X\).
We check both the consistency of \(logit(Y\ge j| X) - logit(Y\ge i|X)\) at different \(X\) levels
Or we can check the parallelism of \(logit(Y\ge j| X) - logit(Y\ge j|X+k)\) for \(Y = 1, \cdots, J\)
3. Method for PO is not met (?)#
When analyzing ordinal data where PO is not met, the Wilcoxon test may still work OK but it will not be optimal.
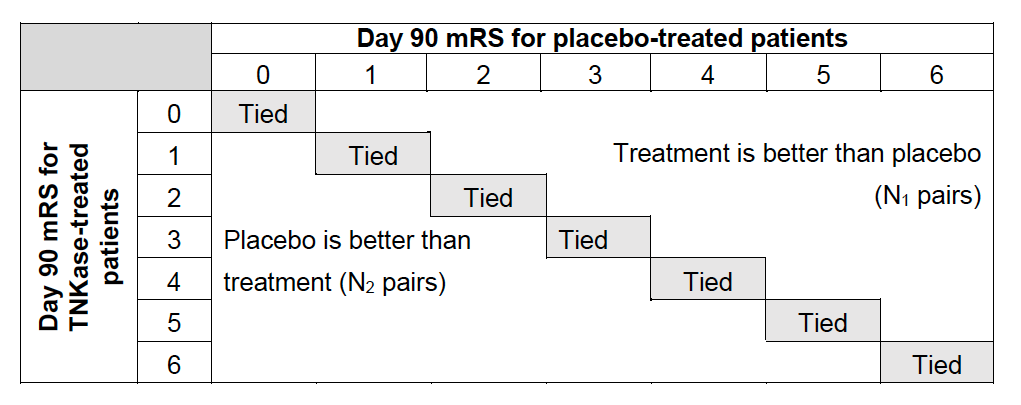
One way to generate a non-parametric version of OR (called Wilcoxon Mann Whitney Generalized OR [WMW GenOR]) is introduced in [Agresti, 1980] and later discussed in [Churilov et al., 2014]. [O’Brien and Castelloe, 2006] offered a way to eliminate ties and apply Agresti’s formula directly.
Note: this statistic isn’t really an “odds ratio”, rather it’s an odds per its mathematic definition
WMW GenOR test statistic is defined as
 \[\hat{\alpha} = \sum_{j>i} p_{1i}p_{2j}/\sum_{j<i}p_{1i}p_{2j}\]
\[\hat{\alpha} = \sum_{j>i} p_{1i}p_{2j}/\sum_{j<i}p_{1i}p_{2j}\]where \(p_{1i} = N_{1i}/\sum_i N_{1i}\) and \(p_{2i} = N_{2i}/\sum_i N_{2i}\)
which follows normal distribution with mean \(\alpha = Pr(Y_2 > Y_1)/Pr(Y_1 > Y_2)\) and variance
\[\hat{\sigma}^2 = \left\{\frac{1}{N_1}\sum_{j}p_{ij}\left(\hat{\alpha}\sum_{i<j}p_{2i} - \sum_{i>j}p_{2i}\right)^2 + \frac{1}{N_2}\left(\hat{\alpha}\sum_{i>j}p_{1i} - \sum_{i<j}p_{2i}\right)^2\right\} \Bigg/ \left(\sum_{i>j}p_{1i}p_{2j}\right)^2\]Furthermore, with patients being stratified into total \(M\) strata, the logrithm of test statistic can be written as
\[\log(\hat{\alpha}) = \sum_m^M \hat{\alpha}_m^2 \log\hat{\alpha}_m/\hat{\sigma}_m^2\Bigg/ \sum_{m}^M\hat{\alpha}_m^2/\hat{\sigma}_m^2\]with variance
\[\hat{\sigma}^2 = \left(\sum_m^M\hat{\alpha}_m^2/\hat{\sigma^2_m}\right)^{-1}\]However, I think as long as it uses Wilcoxon type of method, it actually assumes PO in the data
Sample size calculation with ordinal outcome#
Method 1: with proportional odds assumption [Whitehead, 1993]#
Let \(Q_{ie\text{ or }c} = \sum_{u=1}^i p_{ue\text{ or }c}, \text{for } i = 1,\cdots, k-1\)
Log odds ratio at cutoff \(i\) is defined as \(\theta_{iR} = \log\left\{\frac{Q_{ie}(1-Q_{ic})}{(1-Q_{ie})Q_{ic}}\right\}\)
Proportional odds assumption says: \(\theta_{iR} = \theta_R = \frac{Q_{e}(1-Q_{c})}{(1-Q_{e})Q_{c}}\) for all \(i = 1, \cdots, k-1\)
Basic steps#
Set up the assumption for outcome distribution#
Assume the percentages at the most commonly used cutoff (e.g. mRS \(\le\) 2 vs > 2)
Based on this assumption, calculate the common odds ratio
With the assumption of proportional odds, calculate the percentages for each ordinal category and the full distribution of the ordinal outcome can be obtained accordingly
Sample size calculation#
using normal approximation
where
\(A = n_c/n_e\), is the randomization ratio between control and treated arms
\(\theta_R\) is the log of the common odds ratio for treated vs control arm
\(z_{\alpha/2} = \Phi^{-1}(1-\alpha/2), z_{\beta} = \Phi^{-1}(1-\beta)\)
\(\bar{p}_i = \frac{p_{ie} + p_{ic}}{2}\) for \(i= 1, \cdots, k\)
Method 2: without PO assumtion [Zhao et al., 2008]#
Link to notes.
Method 3: without PO assumption [Tang, 2011]#
Exact variance method for the size and power calculation for theWilcoxon–Mann–Whitney test for ordered categorical data.
Notes to be done
Resources for Ordinal Regression Models#
General references#
https://hbiostat.org/bib/ordinal.html which includes tutorials such as the one by Susan Scott et al.
Alan Agresti. Generalized odds ratios for ordinal data. Biometrics, pages 59–67, 1980.
Leonid Churilov, Sarah Arnup, Hayden Johns, Tiffany Leung, Stuart Roberts, Bruce CV Campbell, Stephen M Davis, and Geoffrey A Donnan. An improved method for simple, assumption-free ordinal analysis of the modified rankin scale using generalized odds ratios. International Journal of Stroke, 9(8):999–1005, 2014.
Ralph G O’Brien and John Castelloe. Exploiting the link between the wilcoxon-mann-whitney test and a simple odds statistic. In Proceedings of the Thirty-first Annual SAS Users Group International Conference, 209–31. Citeseer, 2006.
Yongqiang Tang. Size and power estimation for the wilcoxon–mann–whitney test for ordered categorical data. Statistics in Medicine, 30(29):3461–3470, 2011.
John Whitehead. Sample size calculations for ordered categorical data. Statistics in medicine, 12(24):2257–2271, 1993.
Yan D Zhao, Dewi Rahardja, and Yongming Qu. Sample size calculation for the wilcoxon–mann–whitney test adjusting for ties. Statistics in medicine, 27(3):462–468, 2008.
